وایت بوردی رو برای استفاده شاگردانم در کلاس طراحی کردم که جهت دانلود در این پست میذارم
این وایت بورد به دو صورت سیاه و سفید و رنگی طراحی شده و میتونید در سایز A4 یا A3 پرینت بگیرید سپس دو طرف اون رو طلق(تلق) شفاف بچسبونید تا بچه ها بتونن با استفاده از ماژیک وایت بورد روی اون بنویسن و میتونید چسب های نواری تزیینی برای زیباتر شدن کار دورتادور اون رو بچسبونید
امیدوارم مفید باشه


فایل رنگی
فایل سیاه و سفید
جمع کسرها
رای جمع کسرها باید این سه مرحله را انجام دهیم:
- مرحله ۱: اطمینان حاصل کنید که مخرج ها یکسان هستند
(اگر مخرجها برابر نبودند مخرج مشترک میگیریم)
- مرحله ۲: یکی از مخرجها را می نویسیم و صورت کسرها را با هم جمع می کنیم
- مرحله ۳: ساده کردن جواب(در صورت نیاز)
مثال ۱: کسرهای زیر را جمع کنید:
- مرحله ۱: چون مخرج ها یکسان هستند پس به مرحله ۲ می رویم.
- مرحله ۲: یکی از مخرجها را می نویسیم و صورت کسرها را با هم جمع می کنیم.
- مرحله ۳: کسر را ساده می کنیم که در اینجا نیازی به ساده کردن نیست.
مثال ۲: کسرهای زیر را جمع کنید.
- مرحله ۱: چون مخرج ها یکسانند (هردو 8 هستند) پس به مرحله ۲ می رویم.
- مرحله ۲: یکی از مخرجها را می نویسیم و صورت کسرها را با هم جمع می کنیم.
- مرحله ۳: کسر را ساده می کنیم که در اینجا نیازی به ساده کردن نیست
ولی میتوان آن را بصورت عدد مخلوط نوشت.
نکته: اگر مخرج های کسرها برابر نبودند ابتدا مخرج مشترک میگیریم.
مثال ۳: کسرهای زیر را جمع کنید.
چون مخرجها برابر نیستند پس مخرج مشترک میگیریم و یکی از مخرجها را نوشته و
صورتها را با هم جمع میزنیم
جواب نهایی یعنی ۵/۸ را نمیتوان ساده کرد.
مساحت لوزي
مساحت ذوزنقه
ریاضی ششم اولویت عملیات جبری
رياضي ششم فصل پنجم زاويه
|
كتاب هاي درسي پايه ششم دوره ابتدايي |
|
|
عنوان
|
دانلود |
سال تحصيلي 97-96 | ||||||||||||||||||||||||||||||||||||||||
|
فارسی كد كتاب : 34 (96/04/04) |
|
|||||||||||||||||||||||||||||||||||||||||
|
نگارش فارسی كد كتاب :34/1 (96/04/04) |
فایل بخش های کتاب:
|
|
||||||||||||||||||||||||||||||||||||||||
|
رياضی كد كتاب :34/6 (96/04/04) |
|
|||||||||||||||||||||||||||||||||||||||||
|
آموزش قرآن كد كتاب :34/4 (20/03/96) |
|
|
||||||||||||||||||||||||||||||||||||||||
|
علوم تجربی كد كتاب :34/2 (96/04/04) |
فایل کامل کتاب:
|
|
||||||||||||||||||||||||||||||||||||||||
|
هدیه های آسمان كد كتاب :34/3 (23/05/95) |
فایل کامل کتاب:
|
|
||||||||||||||||||||||||||||||||||||||||
|
کتاب کارو فناوری كد كتاب :34/10 (96/04/04) |
فایل بخش های کتاب:
|
|
||||||||||||||||||||||||||||||||||||||||
|
مطالعات اجتماعی
(24/04/97) |
فایل بخش های کتاب:
|
 |
||||||||||||||||||||||||||||||||||||||||
|
کتاب کارتفکرو پژوهش كد كتاب :34/8 (96/04/04) |
|
|||||||||||||||||||||||||||||||||||||||||
| ضمیمه هدیه های آسمان ( ویژه اهل سنت) كد كتاب : 34/7 (96/04/27) |
فایل بخش های کتاب:
|
|
||||||||||||||||||||||||||||||||||||||||
| هدیه های آسمان (ویژه اقلیت های دینی) كد كتاب : 34/9 (96/04/27) |
فایل کامل کتاب:
|
|
||||||||||||||||||||||||||||||||||||||||
واحد طول قابل تبدیل به واحد سطح نیست .
واحد سطح قابل تبدیل به واحد حجم نیست . چرا ؟
چون واحد طول فقط یک بعد طول دارد ، واحد سطح دو بعدی است و طول وعرض دارد.
واحد حجم سه بعدی است و طول و عرض و ارتفاع دارد .
واحد طول ، پاره خط است .
واحد مساحت ، مربع است .
واحد حجم مکعب است .
این واحدها قابل تبدیل به هم نیستند .
معنی کسر : هرگاه از یک واحد کامل، جزیی از آن ، مورد نظر باشد، آن را به صورت کسر نمایش می دهیم.
هر کسر از سه قسمت تشکیل شده است : صورت، مخرج و خط کسری
کسر مساوی با صفر : هر کسری که صورت آن صفر باشد مساوی صفر است.
کسر کو چک تر از واحد : کسری که صورت آن از مخرجش کوچک تر باشد کسر کوچک تر از واحد می گویند.
کسر بزرگ تر از واحد : کسری که صورت آن از مخرجش بزرگ تر باشد کسر بزرگ تر از واحد می گویند.
کسر واحد : کسری که صورت و مخرج آن مساوی باشند کسر واحد می گویند. کسر واحد همیشه مساوی یک است.
عدد مخلوط : اگر صورت کسر از مخرج بزرگ تر باشد، یعنی چند واحد کامل و جزئی از آن مورد نظر باشد باید آن را به صورت عدد مخلوط نشان دهیم.
روش تبدیل کسر به عدد مخلوط : اگر کسر بزرگ تر از واحد باشد، (صورت از مخرج بزرگ تر باشد) برای به دست آوردن تعداد واحد های کامل و کسری از واحد کامل، صورت کسر را بر مخرج آن تقسیم می کنیم. خارج قسمت را در عدد صحیح ، و باقی مانده را در صورت ، و مخرج همان قبلی است.
توجه : صورت کسر را بر مخرج آن تقسیم می کنیم. خارج قسمت را در عدد صحیح ، و باقی مانده را در صورت ، و مخرج همان مخرج قبلی می باشد.
نمایش کسر روی محور اعداد : در محور هر واحد را به اندازه ی مخرج کسر تقسیم بندی می کنیم و عدد مورد نظر را روی محور نشان می دهیم.
توجه : مخرج هر کسر نشان می دهد که هر واحد را به چند قسمت مساوی تقسیم می کنیم.
کسرهای مساوی : اگر صورت ومخرج کسری را در عدد طبیعی بزرگ تر از یک ضرب کنیم ، کسر مساوی با آن به دست می آید.
روش مقایسه ی کسرها :
حالت اول : در کسرهایی که مخرج آن ها مساوی اند، کسری بزرگ تر است که صورت آن بزرگ تر باشد.
حالت دوم : در کسرهایی که صورت آن ها مساوی اند، کسری بزرگ تر است که مخرج آن کوچک تر باشد.
حالت سوم : برای مقایسه کسرهایی که نه صورت های برابر و نه مخرج های برابر دارند باید هر دو کسررا هم مخرج نماییم بعد صورت هر کدام بزرگ تر باشد آن کسر بزرگ تر است.
حالت چهارم : مقایسه عددهای مخلوط : در مقایسه عددهای مخلوط ابتدا قسمت های صحیح، سپس قسمت های کسری را باهم مقایسه می کنیم.
ساده کردن کسرها :
روش اول:صورت ومخرج کسر رابه صورت حاصل ضرب دو عدد می نویسیم.اگرکسر ساده شدنی
باشد،عدد مشترک در صورت و مخرج راحذف می کنیم تا کسری مساوی با آن به دست آید.
روش دوم:برای ساده کردن کسرکافی است که صورت ومخرج آن را هم زمان بریک عدد طبیعی تقسیم کنیم واین عمل راتا جایی ادامه دهیم که که دیگر صورت و مخرج به طور مشترک بر هیچ عددی قابل قسمت نباشند به این ترتیب کسر به ساده ترین صورت ممکن تبدیل می شود.
توجه 1 : اگر صورت و مخرج کسری را بر هر عدد طبیعی بزرگ تر از یک تقسیم کنیم. کسر مساوی با آن به دست می آید.
توجه 2 : در ساده کردن کسرها هر چه صورت و مخرج را بر عدد های بزرگ تری تقسیم کنیم، ساده کردن سریع تر انجام می شود.
جمع و تفریق کسرها :
به طور کلی شرط لازم برای جمع یا تفریق چند کسرآن است که کسرها هم مخرج باشند. وقتی مخرج ها یکی باشد، یکی از آن ها را نوشته و صورت ها را با توجه به علامت بین کسر ها جمع یا کم می کنیم.
توجه : در جمع وتفریق عددهای مخلوط، ابتدا قسمت های صحیح و سپس قسمت های کسری را باهم جمع یا تفریق می کنیم.
ضرب اعداد مخلوط : به طور کلی برای ضرب اعداد مخلوط، ابتدا باید آن ها را به کسر تبدیل کنیم پس از ساده کردن صورت ها با مخرج ها، حاصل ضرب را به دست می آوریم.
تقسیم کسرها : برای انجام تقسیم دو کسر ابتدا تقسیم را به ضرب تبدیل می نماییم، به این ترتیب که کسر اول را نوشته و به جای علامت تقسیم ضرب می گذاریم و معکوس کسر دوم را می نویسیم وبعد صورت را به صورت و مخرج را به مخرج ضرب می کنیم.
جمع و تفریق کسرها به کمک محور:
1- ابتدا محور را رسم کرده و به اندازه ی مخرج کسر، واحدها را تقسیم بندی می کنیم.
2- اگر مخرج ها برابر نباشند مخرج مشترک گرفته سپس محور را تقسیم بندی می کنیم.
3- روی محور اولین کسر را با خط نمایش می دهیم.
4- در جمع به اندازه ی کسر دوم از انتهای کسر اول جلو می رویم نقطه ی به دست آمده جواب سوال است.
در تفریق به اندازه ی کسر دوم از انتهای کسر اول به سمت صفر محور برمی گردیم تا جواب به دست آید.
نمایش عددهای اعشاری: اعداد اعشاری اعدادی هستند که از دو قسمت صحیح و اعشاری تشکیل شده اند.مانند4/35 که قسمت صحیح آن 4و قسمت اعشاری آن 35 می باشد.
به کسرهایی که مخرج آن ها 10 یا 100 یا 1000 یا ... باشد کسر اعشاری می گویند.
توجه : در عددهای اعشاری اولین رقم بعد از ممیز دهم ، دومین رقم صدم ، سومین رقم هزارم و... می گویند.
روش تبدیل کسر به عدد اعشاری :
حالت اول) برای تبدیل کسرهایی که مخرج آنها 10 یا 100 یا 1000 یا ... می باشد، ابتدا صورت کسر را نوشته و سپس به تعداد صفرهای مخرخ از سمت راست عدد ، جدا کرده و ممیز می زنیم.
حالت دوم) برای تبدیل کسرهایی که مخرج آنها 10 یا 100 یا 1000 یا ... نیست باید صورت ومخرج را در عددی ضرب کنیم تا مخرج کسر یکی از عددهای 10 یا 100 یا 1000 یا ... شود .
حالت سوم) اگر مخرج یک کسر به عددهای 10 یا 100 یا 1000 یا ...تبدیل نشد در این صورت باید صورت کسر را بر مخرجش تقسیم کنیم و خارج قسمت را تا یک رقم اعشار و یا بیشتر به دست آوریم.
روش مقایسه ی دو عدد اعشاری : ابتدا قسمت های صحیح را باهم مقایسه می کنیم، عددی بزرگ تر است که قسمت صحیح آن بزرگ تر باشد. در صورت مساوی بودن قسمت های صحیح ، قسمت های اعشاری آن ها را به ترتیب : به این صورت که ابتدا رقم های مرتبه ی دهم، سپس رقم های مرتبه ی صدم، سپس رقم های مرتبه ی هزارم ,… را باهم مقایسه می کنیم.
روش تبدیل عددهای اعشاری به کسر : ابتدا عدد را بدون ممیز در صورت کسر می نویسیم ، تعداد رقم های قسمت اعشار ، نشان دهنده ی تعداد صفرهای جلوی یک در مخرج است.
توجه1 : اگر در عددهای اعشاری ، بعد از آخرین رقم اعشاری به تعداد دلخواه صفر بگذاریم عدد هیچ تغییری نمی کند. از این خاصیت در جمع و تفریق یا پیش روی در تقسیم اعشاری استفاده می کنیم.
مثال : ... = 75/300= 75/30= 75/3
توجه 2 : توجه کنید اگر در بین رقم های یک عدد اعشاری صفر قرار دهیم عدد تغییر می کند به طور مثال عددهای 25/2 و 25/02برابر نیستند.
جمع اعداد اعشاری
در جمع اعداد اعشاری مراحل زیر را طی می کنیم:
1-بهتر است عدد بزرگتر را بالا قرار دهیم.
2-قسمت های صحیح را زیر هم می نویسیم یعنی : یکان زیر یکان، دهگان زیر دهگان و ...
3- ممیز را در زیر ممیز می نویسیم.
4-قسمت های اعشاری را زیر هم می نویسیم یعنی دهم زیر دهم، صدم زیر صدم و...
5- مانند جمع معمولی ، عمل جمع را انجام می دهیم.
تفریق اعداد اعشاری
تفریق اعداد اعشا
در تفریق اعداد اعشاری مراحل زیر را طی می کنیم:
1-باید حتما عدد بزرگتر را بالا قرار دهیم.
2-قسمت های صحیح را زیر هم می نویسیم یعنی : یکان زیر یکان، دهگان زیر دهگان و ...
3- ممیز را در زیر ممیز می نویسیم.
4-قسمت های اعشاری را زیر هم می نویسیم یعنی دهم زیر دهم، صدم زیر صدم و...
5- مانند تفریق معمولی ، عمل تفریق را انجام می دهیم.
ضرب اعداد اعشاری
برای ضرب اعداد اعشاری ، دو عدد را بدون در نظر گرفتن ممیز در زیر هم نوشته و عمل ضرب را انجام می دهیم سپس به تعداد رقم های اعشاری در حاصل ضرب از سمت راست به چپ رقم جدا کرده و ممیز می زنیم.
تقسیم اعداد اعشاری
تقسیم اعداد اعشاری بر دو نوع است: تقسیم اعشاری نوع اول – تقسیم اعشاری نوع دوم
تقسیم اعشاری نوع اول : یعنی مقسوم عدد اعشاری است ولی مقسوم علیه عدد صحیح.
تقسیم اعشاری نوع دوم : یعنی مقسو علیه عدد اعشاری می باشد.
روش حل تقسیم اعشاری نوع اول :
1-ابتدا از ممیز یک خط راست می کشیم . این خط نشان دهنده تمام ممیزهایی است که در میان اعداد قرار می گیرد.
2-تقسیم را مانند تقسیم معمولی انجام می دهیم.
3-وقتی به ممیز رسیدیم در خارج قسمت ممیز میزنیم.
4-در پایان ، در باقیمانه ار روی خط، ممیز می زنیم.
روش حل تقسیم اعشاری نوع دوم
الف ) ابتدا باید مقسوم و مقسوم علیه را در 10 ویا 100 ویا 1000 ویا... ضرب کنیم. تا ممیز مقسوم علیه از بین برود و سپس تقسیم را انجام می دهیم.
توجه : (اگر مقسوم علیه یک رقم اعشار داشته باشد در 10 ضرب می کنیم- اگر مقسوم علیه دو رقم اعشار داشته باشد در 100 ضرب می کنیم ... )
ب ) در پایان کار باقیمانده را بر عددی که مقسوم و مقسوم علیه ضرب کردیم تقسیم می کنیم.
نمایش عدد اعشاری روی محور : برای نشان دادن یک عدد اعشاری روی محور ، به ترتیب مراحل زیر را در نظر می گیریم :
1- محور اعداد را رسم می کنیم.
2- هر واحد را با توجه به قسمت اعشاری به ( 10 یا 100 یا .. ) قسمت مساوی تقسیم می کنیم مثلا اگر دهم باشد هر واحد را به 10 قسمت مساوی تقسیم می کنیم.
روی قسمت های تقسیم شده، قسمت اعشاری را مشخص می کنیم.
مقدمه
فاصله ی دو نقطه : فاصله ی دو نقطه طول پاره خطی است که دو نقطه را به هم وصل می کند.(تمرین 3 ص 60 کتاب)
فاصله ی نقطه تا خط : کوتاه ترین فاصله ی یک نقطه تا یک خط ، طول خطی است که از آن نقطه بر خط عمود می شود.(تمرین 4 ص 60 کتاب)
تعریف نیم ساز : نیم ساز خطی است که از راس زاویه می گذرد و زاویه را به دو قسمت مساوی تقسیم می کند.
توجه :فاصله ی هر نقطه روی نیمساز یک زاویه از دو ضلع آن زاویه به یک فاصله است.
انواع مثلث :
1-مثلث متساوی الاضلاع : مثلثی است که سه ضلع و سه زاویه ی مساوی دارد. و اندازه ی هر سه زاویه آن 60 درجه است.
2-مثلث متساوی الساقین : مثلثی که دو ضلع (دوساق)مساوی دارد.و دو زاویه ی مجاور آن دو ضلع برابرند.
3-مثلث قائم الزاویه : مثلثی که یک زاویه ی قائمه (90 درجه ) دارد. به ضلع روبرو به زاویه ی قائمهوتر می کویند.
4-مثلث قائم الزاویه ی متساوی الساقین : مثلثی که یک زاویه ی قائمه دارد و دو ضلع زاویه ی قائمه ی آن برابرند.
5-ملث مختلف الاضلاع : اندازه ی ضلع های آن باهم فرق دارند.
ارتفاع خارجی :در مثلث مختلف الاضلاعی که یک زاویه ی باز دارد یک ارتفاع خارجی وجود دارد.
توجه : مجموع زاویه های داخلی هر مثلث 180 درجه می باشد.
ارتفاع مثلث : پاره خطی است که از یک راس ، عمود بر ضلع روبرو رسم می شود.
توجه : در هر مثلث ، اندازه ی پاره خطی که وسط های دو ضلع یک مثلث را به هم وصل می کند نصف ضلع سوم است. (تمرین 2 ص 48 کتاب درسی)
روی یک نیم خط یک نقطه بگذاریم 2 نیم خط به دست می آید
اگر روی یک نیم خط 2 نقطه بگذاریم 4 نیم خط به دست می آید
اگر روی یک نیم خط 3 نقطه بگذاریم 6 نیم خط به دست می آید
اگر روی یک نیم خط 4 نقطه بگذاریم 8 نیم خط به دست می آید
اگر روی یک نیم خط 5 نقطه بگذاریم 10 نیم خط به دست می آید
دقت شود با روش بالا تعداد نیم خط ها به دست می آید نه تعداد پاره خط ها.
××××××××××××××××××××××××××××××××××××××××××××××××××××××××××
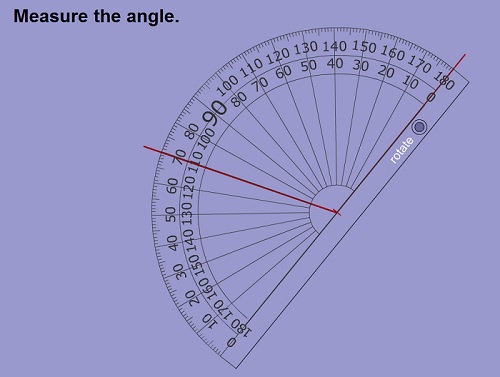
اندازه گیری زاویه :
-وسیله ی اندازه گیری زاویه نقاله نام دارد.
-واحد استاندارد اندازه گیری زاویه درجه نام دارد.
-یک درجه برابر ( یک ، سیصدو شصتم )![]() یک دایره ی کامل است. به عبارت دیگر اگر یک دایره ی کامل را به 360 قسمت مساوی تقسیم کنیم هر قسمت آن یک درجه است.
یک دایره ی کامل است. به عبارت دیگر اگر یک دایره ی کامل را به 360 قسمت مساوی تقسیم کنیم هر قسمت آن یک درجه است.
-معنای زاویه : هر زاویه از دو نیم خط تشکیل شده است ، به نقطه ی مشترک این دونیم خط راس زاویه می گویند ، و به هر یک از این دو نیم خط ضلع زاویه می گویند.
روش اندازه گیری زاویه با نقاله : (تمرین 5 ص 60 کتاب)
نقطه ی شروع (صفر) نقاله را روی نقطه ی مشترک دو ضلع زاویه(راس زاویه) قرار می دهیم دقت کنیم که یک ضلع زاویه و خط شروع نقاله بر هم منطبق باشند. ضلع دیگر زاویه بر روی نقاله نشانگر اندازه ی زاویه می باشد.
توجه : برای محاسبه ی مجموع زاویه های چند ضلعی ها ، چندتا از قطر های چند ضلعی را طوری رسم کنیم که همدیگر را قطع نکنند و شکل نیز به چند مثلث تبدیل شود حالا با ضرب تعداد مثلث ها در 180 درجه، مجموع زاویه های آن چند ضلعی به دست می آید. (تمرین 4 ص 59 کتاب درسی شش ضلعی)
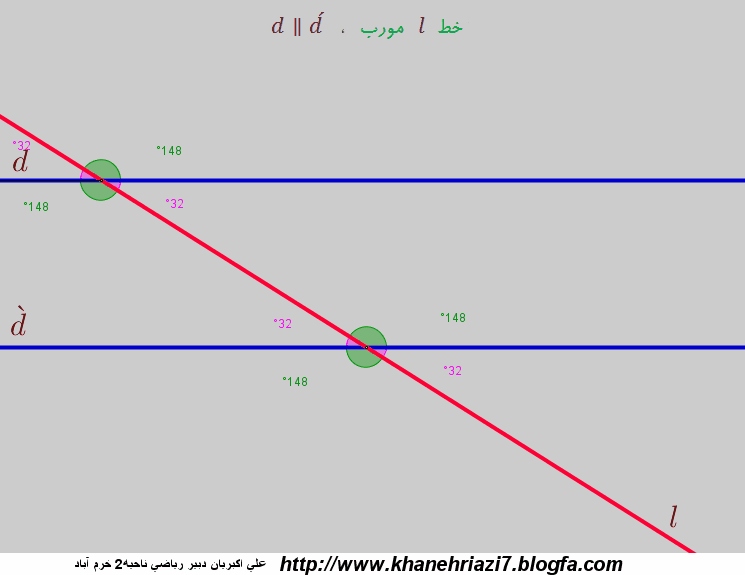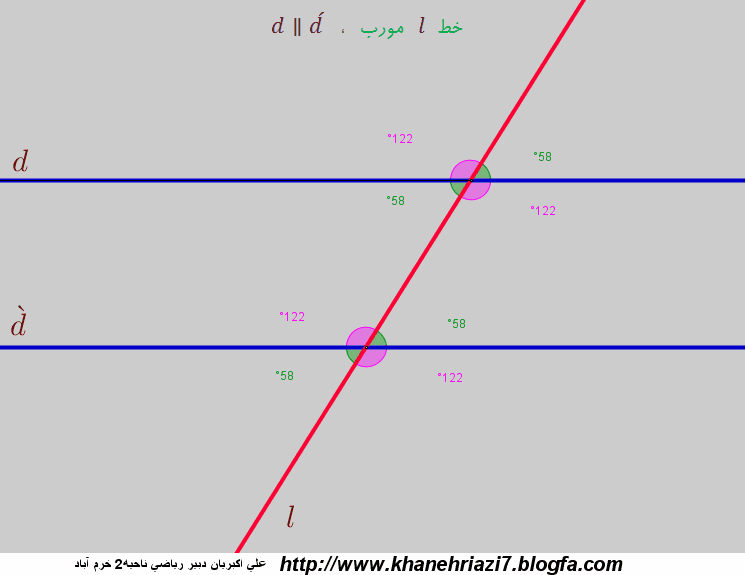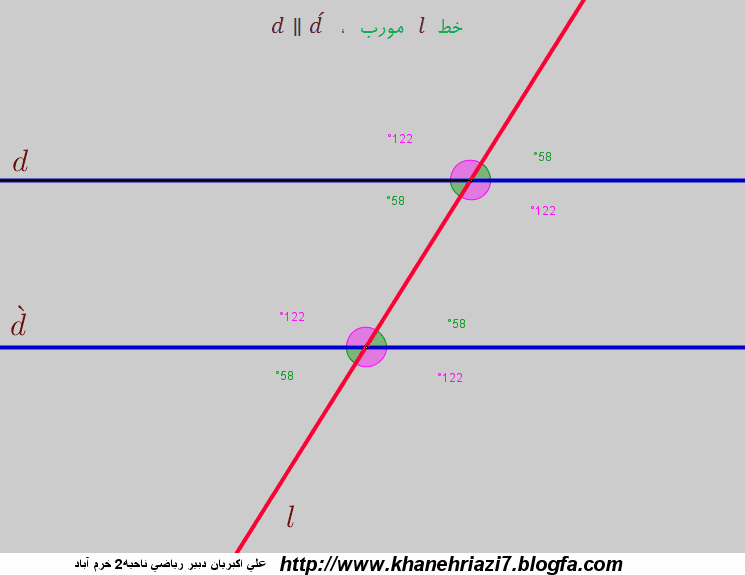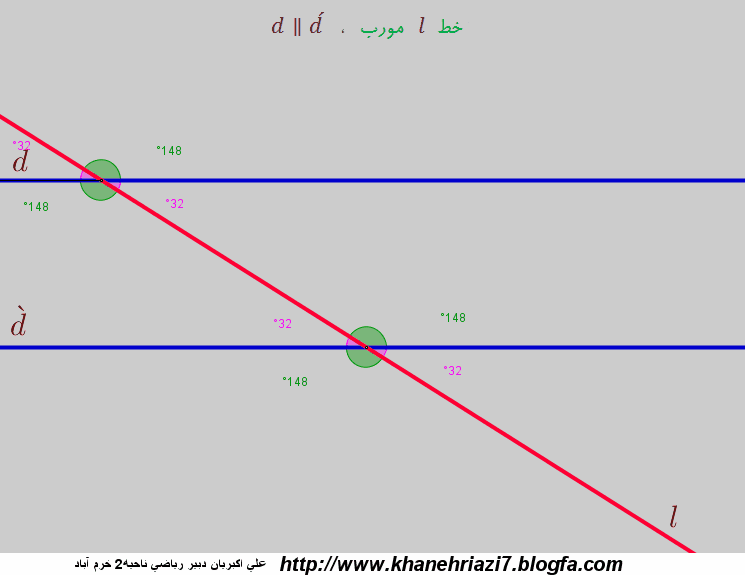
-ص 55 کتاب درسی تمرین 4 : اگر یک خط مورب دوخط موازی را قطع کند زاویه های مشخص شده روی شکل همیشه باهم برابر هستند.
-ص 55 کتاب درسی تمرین 5 : همه ی زاویه هایی که راس آن ها روی دایره قرار داشته باشند و روبروی یک کمان از دایره باشند باهم مساوی هستند.
انواع زاویه: زاویه ی رست یا قائمه که اندازه ی آن 90 درجه است.- زاویه ی تند که اندازه ی آن کمتر از 90 درجه است. – زاویه ی باز که اندازه ی آن بیشتر از 90 درجه است. زاویه ی نیم صفحه که اندازه ی آن 180 درجه است.
-زاویه های متقابل به راس: اگر دو خط همدیگر را قطع کنند 4 زاویه به دست می آید که دو به دو برابر هستند این زاویه ها را متقابل به راس می گویند.
ویژگی های دو زاویه ی متقابل به راس: (تمرین 6 ص 60 کتاب درسی)
1-دو زاویه ی متقابل به راس همیشه مساوی هستند.
2- راس آن ها روی هم قرار دارند.یعنی راس دو زاویه باید بر هم منطبق باشد.
3- ضلع هر یک در ادامه ی ضلع زاویه ی دیگر است.
دو زاویه ی متمم و مکمل : (تمرین 7 ص 60 کتاب درسی)
دو زاویه ی متمم :به دو زاویه ای که مجموع آن ها 90 درجه باشد دو زاویه ی متمم می گویند. مانند دوزاویه 20 درجه و 70 درجه . 90=20+70
دو زاویه ی مکمل : به هر دو زاویه ای که مجموع آن ها 180 درجه باشد دو زاویه ی مکمل می گویند. مانند دو زاویه ی 130 درجه و 50 درجه. 180=50+130
تبدیل واحد : (تمرین یک ص 60 کتاب و تو ضیح ص 44 کتاب درسی)
برای تبدیل واحد های کوچک به بزرگ از ضرب در 10 ، 100 ، 1000 و... استفاده می کنیم و برای تبدیل واحدهای بزرگ به کوچک از تقسیم عدد بر 10 ، 100 ، 1000 و ..... استفاده می کنیم. سانتی متر210 = 1/2 متر
مقدمه
گاهی لازم است که اعداد را به صورت تقریبی بیان کنیم تا انجام محاسبه روی آن ها ساده تر شود در این صورت مقدار محاسبه شده با مقدار واقعی برابر نیست ولی به آن نزدیک است.به عنوان مثال اگر وزن امین 48/358 کیلو گرم باشد بهتر است بگوییم وزن او تقریبا 48 کیلوگرم است. یا اگر سن مهدی 14 سال و 3 ماه و 17 روز است بهتر است بگوییم سن او تقریبا 14 سال است. پس نتیجه میگیریم که در زندگی روزمره با موضوعاتی سر و کار داریم که از عددهای تقریبی به جای عددهای واقعی و دقیق استفاده میکنیم.(تمرین یک ص 80 کتاب درسی )
انواع تقریب زدن : تقریب زدن بر دو نوع است : قطع کردن – گرد کردن
روش قطع کردن : در این روش سمت راست تقریب یعنی آن عددهایی که ارزش مکانی آنها کم تر از تقریب داده شده است به صفر تبدیل می کنیم. ( تمرین 3 ص 80 کتاب درسی )
مثال : مقدار تقریبی عدد 4268/315با تقریب کم تر از 100 با روش قطع کردن چیست؟ برای بدست آوردن جواب همه ی اعدادی که کمتر از مرتبه ی صدگان هستند حذف می کنیم و بجای آنها صفر می گذاریم مثال :
4200 =4200/00=4268/315
توجه 1 : صفرهای بعد از ممیز تاثیری در عدد نداشته به همین دلیل می توان آنها را حذف کردمثال: 4200=4200/00
توجه 2 : صفرهای قبل از ممیز دارای ارزش هستند و نباید حذف کنیم.
روش تقریب زدن اعداد کسری به روش قطع کردن و گرد کردن: ابتدا صورت کسر را بر مخرج کسر تقسیم می کنیم - اگر تقسیم را تا یک رقم اعشار ادامه دهیم یعنی جواب را با تقریب کم تر از 0/1 بدست آورده ایم - اگر تقسیم را تا 2 رقم اعشار ادامه دهیم یعنی جواب را با تقریب کم تر از 0/01 بدست آورده ایم - اگر تقسیم را تا 3رقم اعشار ادامه دهیم یعنی جواب را با تقریب کم تر از 0/001 بدست آورده ایم.
روش گرد کردن:برای این که در استفاده از عددهای تقریبی خطای کم تری داشته باشیم و هم چنین مقدار تقریبی عدد به مقدار واقعی آن نزدیک تر باشد بهتر است از روش گرد کردن استفاده کنیم. در این روش ابتدا به رقم جلوی تقریب دقت می کنیم ، اگر این عدد بزرگتر ویا مساوی 5 (5،6،7،8،9) باشد یک رقم به رقم تقریب اضافه می کنیم و در غیر این صورت مانند روش قطع کردن رقم های جلوی تقریب را به صفر تبدیل می کنیم مثال : 3/8=3/76 ( تمرین 4 ص 80 کتاب درسی )
تفاوت بین قطع کردن و گرد کردن : درروش قطع کردن سرعت انجام محاسبات بیشتر است ولی در روش گرد کردن دقت انجام محاسبات بیشتر است . استفاده از این روش ها به اهمیت دقت یا سرعت محاسبات بستگی دارد.
توجه:اگر رقم سمت راست تقریب کم تر از5 باشد جواب به دست آمده با هردو روش قطع کردن و گرد کردن مساوی می شود.
استفاده از تقریب در انجام عملیات : استفاده از عددهای تقریبی می تواند تصور خوبی از پاسخ عملیات مختلف به شما بدهد. بهتر است قبل از انجام عملیات پاسخ را تقریب بزنید. در صورتی که پاسخ عملیات شما با عدد تقریبی به دست آمده فاصله ی زیادی داشته باشد بهتر است دوباره راه حل خود را بررسی کنید تا دلیل این اختلاف و اشتباه خود را بیابید.
به طور خلاصه در قطع کردن به معانی زیر دقت شود :
- با تقریب کم تر از یک یعنی : تمامی اعداد و ارقامی که کمتر از مرتبه ی یکان قرار دارند ارزشی ندارند و ما آن ها را حذف می کنیم و به جای آن ها صفر می گذاریم.
- با تقریب کم تر از 10 یعنی : تمامی اعداد و ارقامی که کمتر از مرتبه ی دهگان قرار دارند ارزشی ندارند و ما آن ها را حذف می کنیم و به جای آن ها صفر می گذاریم.
- با تقریب کم تر از 100 یعنی : تمامی اعداد و ارقامی که کمتر از مرتبه ی صدگان قرار دارند ارزشی ندارند و ما آن ها را حذف می کنیم و به جای آن ها صفر می گذاریم.
- با تقریب کم تر از 1000 یعنی : تمامی اعداد و ارقامی که کمتر از مرتبه ی هزارگان قرار دارند ارزشی ندارند و ما آن ها را حذف می کنیم و به جای آن ها صفر می گذاریم.
- با تقریب کم تر از0/1 یعنی : تمامی اعداد و ارقامی که کمتر از مرتبه ی دهم قرار دارند ارزشی ندارند و ما آن ها را حذف می کنیم و به جای آن ها صفر می گذاریم.
- با تقریب کم تر از 0/01یعنی : تمامی اعداد و ارقامی که کمتر از مرتبه ی صدم قرار دارند ارزشی ندارند و ما آن ها را حذف می کنیم و به جای آن ها صفر می گذاریم.
- با تقریب کم تر از0/001یعنی : تمامی اعداد و ارقامی که کمتر از مرتبه ی هزارم قرار دارند ارزشی ندارند و ما آن ها را حذف می کنیم و به جای آن ها صفر می گذاریم.
توجه : در روش گرد کردن اگر عدد جلوی تقریب کم تر از 5 باشد مانند روش های بالا عمل می کنیم.
توجه : در روش گرد کردن اگر عدد جلوی تقریب بیش تر از 5 باشد یک تا به عدد تقریب اضافه می کنیم
![]()

* کاربرد کلیدهای ترکیبی *
(درس کار و فناوری ششم)
جهت دریافت شکل pdf زیر را کلیک نمائید
دانلود


* ارکان تشبیه *
(درس ادبیات ششم)
جهت دریافت شکل PDF زیر را کلیک نمائید
دانلود


* انواع قالب های شعری *
(درس ادبیات ششم)
جهت دریافت شکل PDF زیر را کلیک نمائید
دانلود


* آرایه های ادبی *
(درس ادبیات ششم)
جهت دریافت شکل PDF زیر را کلیک نمائید
دانلود

![]()


* تبدیل واحدها در ریاضی *
( درس ریاضی ششم )
دلنلود
رياضيات شامل علائم، فرمولها، روشهاي ويژه و کتابهاي درسياي است که سخت به نظر ميآيند و خيلي کلمات و اصطلاحات منحصربهفرد هستند. در نتيجه مهم است که از مهارتهاي مطالعهاي استفاده کنيد که اختصاصاً مناسب رياضيات باشد.
1- شما نميتوانيد رياضيات را فقط با خواندن و گوش دادن ياد بگيريد. قسمت زيادي از يادگيري رياضيات به تمرين کردن فعالانه بستگي دارد. اين بدان معني است که شما حتماً بايد همهي تکاليف و وظايف محولهي درسي خود در رياضيات را انجام دهيد. ياد گرفتن چگونگي استفاده از فرمولها و روشها، حياتي است.
2- رياضيات يک موضوع زنجيرهاي است. چيزي که در يک روز معين درس داده ميشود بر اساس آموختههاي روز قبل از آن است. همين که عقب افتاديد، دوباره رسيدن به درس سخت ميشود. آماده شدن براي امتحان، آن هم در دقايق آخر، به شما کمک نخواهد کرد. بايد در همهي کلاسها شرکت کنيد و پابهپاي معلمتان پيش برويد.
3- رياضيات مبحث سختي است که به طور فزايندهاي پيچيده ميشود. شايد لازم باشد که زمان مطالعهی بيشتري براي رياضيات نسبت به ديگر مباحث اختصاص دهيد.
4- سعي نکنيد که روش خود را در رياضيات حفظ کنيد. فرمولها و روشهاي بسيار زيادي در رياضيات وجود دارد. سعي کنيد که بر روشهاي کليدي مسلط شويد. اين کار ميزان اطلاعاتي را که بايد به خاطر بسپاريد کاهش خواهد داد.
5- وقتي روشي را براي حل يک مسئله ياد گرفتيد، دقيقاً همان روش براي ديگر مسائل هم در اغلب موارد ميتواند استفاده شود. وقتي با مسئلهي جديدي روبهرو ميشويد، سعي کنيد آموختههاي قبلي خود را بر مسئلهی جديد اعمال کنيد.
6- فرهنگ لغات رياضي را ياد بگيريد. اغلب کلمهاي که در رياضي مورد استفاده قرار ميگيرد، وقتي در مبحثي غير از رياضي مورد استفاده قرار ميگيرد، معناي متفاوتي ميدهد. کلمات و اصطلاحات جديد رياضي و معناي رياضي آنها را در قسمتهاي خاصي از دفتر خود وارد کنيد.
7- رياضيات مبحثي است که بسياري از دانشآموزان را مضطرب ميکند. داشتن اعتمادبهنفس ميتواند اضطراب شما را کاهش دهد. روشهايی که برای مطالعهی رياضي به شما پیشنهاد میکنیم ميتواند به شما در موفقيت در رياضيات کمک کند. تا زماني که تشخيص ميدهيد به راهکارهايي بيش از اينها نياز داريد، کمک بگيريد و تلاش بسياري بکنيد.
پاورپوینت هوشمند ریاضی ۷ (اول متوسطه ی اول) فصل اول
این فایل مناسب برای تدریس هوشمند در کلاس درس (که همکار محترم هنگام تدریس بوسیله ی آن، لازم است پاسخ برخی فعالیت ها و کار در کلاس ها را با توجه به مشارکت دانش آموزان، در سر کلاس تکمیل کند!) اگر کسی تجربه ی تدریس ریاضی ۷ را داشته باشه، از دیدن این فایل لذت خواهد برد! (خودم که خوشم آمد!) لینک فصل اول: http://s6.picofile.com/file/
کاری از استاد حمید پوزن
فایل چاپی (پی دی اف) فصل اول ریاضی ۷ (وابسته به جزوه ی پاورپوینت فصل اول ریاضی۷، در بالا) که زیپ شده است، به همکاران تقدیم می گردد؛ البته همکاران ابتدا آن را از حالت زیپ خارج کنند! این فایل به دانش آموزان تحویل داده می شود تا قبل از شروع کلاس آن را چاپ کرده و در هنگام تدریس هوشمند، آنرا در کلاس تکمیل نمایند؛ لینک این فایل: http://s6.picofile.com/file/
عوامل ضعف آموزش ریاضی و مشكلات مربوط به آن (2)
در مقاله ی قبلی به عوامل ضعف آموزش ریاضی مربوط به خود دانشآموز ابتدایی و عوامل مربوط یه ضعف کتب درسی پرداختیم. در این مقاله به عوامل ضعف آموزش ریاضی مربوط به روش های آموزش و عوامل مربوط به معلمان ابتدایی می پردازیم.
عوامل ضعف آموزش ریاضی مربوط به روشهای آموزش:
كلاس ریاضی سخت است چون با زبانهای خودش بیان نمیشود بلكه در چارچوب كتاب و روش تدریس معلمان محدود شده است و با حجم زیاد كتاب، معلم نمیتواند مطالب جالب و توضیحات لازم را در مورد تاریخ و نحوهی به كاربردن مطالب تدریس در زندگی را بیان كند.
باید توجه داشته باشیم كه معلم ولو ریاضیدان باشد نمیتواند ادعا كند كه روشی كه در تدریس به كار میبرد بهترین است؛ زیرا ریاضیدانستن یك چیز و ریاضی تدریسكردن چیزی دیگر است اگر روش بنا به منطق بزرگسالان بهتر به نظر آید، معلوم نیست برای دانشآموزان كه هنوز فرایندهای منطقی نزد آنها در حال تحول است مناسب یا مناسبتر باشد.

پروفسور ورتایمر تفكر كودكان را مورد تحقیق قرار داد و آن را در كلاسهای مختلف مطالعه كرد نتیجهای كه از مطالعات خود گرفت این بود كه اغلب شیوههای تدریس كوركورانه است و در كودكان جمود فكری ایجاد میكند و تمرینهای تكراری و پاسخهای ماشینی كه از كودكان توقع دارند، انعطافی را كه فكر سالم نیازمند آن است در كودكان ایجاد نمیكند مبالغه در تكرار مطالب نیز میتواند زیانآور باشد این نوع تربیت خطرناك است زیرا دانشآموزان را وادار میكند كه چشم بسته چیزهایی بگویند یا كارهایی انجام دهند بدون اینكه فكر آنها را به كار بیندازد.
هر چند متأسفانه در كشور ما روشهای آموزش هیچ یك از مواد درسی با روش علمی مورد بررسی قرار نگرفته است، ولی قرائن موجود حكایت از آن دارد ه روش تدریس ریاضیات، مثلاً از روش تدریس زبان فارسی، جغرافیا نظام یافته است با این وجود به عقیده اینجانب تاریخ تعلیم ریاضیات در مجموع رضایتبخش نیست نه تنها بازده تلاشهای مربوط به آموزش در این حیطه ناچیز است، بلكه برخلاف انتظار، فراگیری ریاضیات به رشد فكری دانشآموزان كمك نمیكند.
تصورات منطقی ذهن و به طور كلی هوش انسان زاییدهی درونیشدن اعمال اوست. تشریح حقایق و مفاهیم ریاضی به صورتی كه در روش «تدریس زمانی» معمول است برای كودك كافی نیست مشاهده تصاویر و اشكال و مجموعههایی كه متضمن حقایق و روابط ریاضی باشد نیز چنان كه در روشهای مكاشفهای معمول است مفید فایدهای نیست برای آنكه تصورات حاصله دقیق مفاهیم روشن باشد، دانشآموز باید شخصاً به تجربه و آزمایش بپردازد اشیاء و مسایل را از نزدیك دستكاری كند تا روابط كمیتها را مستقیماً درك نماید.
به عقیده پیاژه آموزش صحیح باعث درونیشدن مطالب ریاضی میشود كه دارای خصوصیات ذیل میباشد:
با توجه به تفاصیل فوق به این نكته میرسیم كه یكی از علتهای ضعف آموزش ریاضی در دوره ابتدایی استفاده نكردن معلمان از روشهای تدریسی است كه متناسب با درس ریاضی باشد یعنی كودكان را واردار میسازد تا فكر كنند و افكار خود را هرچند كه درست نباشد بیان كنند همه میدانیم که به تعداد معلمان دنیا روشهای مختلف تدریس وجود دارد اما همهی روشهای تدریس معمولاً در چند قالب كلی جای میگیرد پس اهمیت دارد كه چه روشی با توجه به شرایط و وضعیت كلاس انتخاب شود كه ما را به بیشترین بهرهوری برساند ولی متأسفانه روشهای برای تدریس این درس مهم معمولاً انتخاب میشود كه آسانترین روش باشد و معمولاً بهترین روش آسانترین روش ارائه درس نمیباشد گاهاً روشهایی انتخاب میشود كه از نظر بزرگسالان روش مناسب تشخیص داده شده ولی میتواند از نظر كودكان بدترین روش برای یادگیری باشد.
علل ضعف آموزش ریاضی كه مربوط به معلمان ابتدایی است:
ریاضی بدون زحمت نیست اما هرگز نگفتهاند ممكن است لذتبخش هم باشد، ریاضی در جامعه ما به اندازه كافی هولانگیز شده و نیازی نیست ما معلمان از آن غول بسازیم و به جای رفع مشكل با رفتار و گفتار خود بر شدت آن بیافزاییم.
چه بخواهیم چه نخواهیم باید این واقعیت را قبول كرد كه علل عدیدهای از ضعفهای آموزشی ریاضی برمیگردد به خود. میتوان عواملی را كه معلمان را در ضعف اموزش ریاضی سهیم میكند به صورت مختصر و به شرح ذیل بیان میکرد:

چند عامل دیگر از عوامل ضعف آموزش ریاضی
با توجه به اینكه خیلی از تمرینات ریاضی را دانشآموزان در منزل انجام میدهند عدم توجه خانواده به این موضوع میتواند از عوامل بهوجودآورنده ضعفهای آموزش درس ریاضی باشد.

اكنون ریاضیات بیش از هر زمان دیگر ملموس شده و نقش حیاتی یافته است در ربع قرن گذشته، ریاضیات و روشهای ریاضی به جزء لاینفك، فراگیر و اساسی علوم و تكنولوژی و اقتصاد تبدیل شده است كه در آستانه قرن بیست و یكم ناتوانی در درك یا به كارگیری ریاضیات نماینگر یك شكاف آموزشی است.
بارها خودمان را عقب افتاده نامیدهایم، اما هرگز سعی نكردهایم در جهت رفع این معضل گامی برداریم چون فكر میكنیم از ما بهترین هستند معلمان از درس نخواندن شاگردان شكایت دارند و دانشآموزان به محض گرفتن نمره بد از معلمان و نحوه تدریس آنها شاكی هستند اكثر والدین هم فكر میكنند این كار از عهدهی انها خارج است در آخر هم همه از زیر بار مسئولیت در میروند و از برعهده گرفتن قسمتی از خطاها، شانه خالی میكنند.
پس به این نتیجه میرسیم كه علل ضعف آموزش درس ریاضی در دوره ابتدایی مختص به یك گروه خاص نیست یعنی مافقط نمیتوانیم معلمان یا طراحان كتب درسی یا دانشآموزان با اولیاء را علت ضعفهای موجود در آموزش ریاضی بدانیم بلكه هر یك به نوعی در این معضل سهیم میباشند كه كم ترین علت ضعف مربوط به درس ریاضی در این دوره برای دانشآموزان میباشد اما به علت نواقص و گاهاً كمكاری یك بخش از این عوامل موجبات مشكلاتی را در راه آموزش درس ریاضی بوجود میآورد كه در خیلی موارد نشناختن علت و یا مسئله همه چیز را خوب و كامل تصور كردن باعث می شود كه اصلاً برروی عوامل ضعف و مشكلات فكری صورت نگیرد و یا حتی مسئله تشخیص داده نشود تا تلاشی برای پاسخ آن صورت گیرد پس در این مقاله با بیان قسمتی از عوامل ضعف و مشكلات آموزشی درس ریاضی به خصوص در استان و عموماً در سطح كشور سعی شده تا همكاران را با ضعفها آشنا نموده و سپس با ارائه راهكارهایی از طرف نویسنده مقاله و به تفكر واداشتن همكاران راهكارهای دیگری نیز از طرف همكاران ارائه و جمعآوری شده تا حداقل از ضعفها كاسته شود.
منبع :سایت تبیان
تجمیع: نسیم گوهری - تنظیم: داودی
عوامل ضعف آموزش ریاضی و مشكلات مربوط به آن (1)
مقدمه:
به محض این كه كودك به مدرسه پا میگذارد با درسی به نام ریاضی آشنا میشود و معلم میگوید: «درس ریاضی را جدی بگیرید و برای فهمیدن آن احتیاج به تمرین بیشتری دارید». همین كلمهی جدی بگیرید برای دانشآموز مشكل آفرین است، زیرا یادگرفته است كه كارهای سخت را جدی بگیرد در نتیجه با ترس به مسایل آن نگاه كرده و ترس از این دارد كه ممكن است آن را خوب یاد نگیرد و این امر مقدمهای است برای دوری كردن و حتی به وجودآمدن نفرت از درس ریاضی در كودكان در صورتی كه روژه گورسانی در مورد ریاضی میگوید: «نخستین وظیفه ریاضیات، ساختن و تحولدادن چیزی به جامعه است كه امروزه كمتر كسی خواستار آن است، یعنی «انسان» انسانی كه بیاندیشد، انسانی كه درست را از نادرست تشخیص دهد، انسانی كه شناخت و انتشار حقیقت را بر بسی چیزها از جمله یك تلویزیون برتری دهد، انسان آزاد نه آدموارهای آهنی»

كسانی كه میخواهند در این عصر یعنی عصر حاكمیت علم فعالیت كنند، لازم است ایدههای تازه را جذب، طرحهای نو را درك و مسایل غیر سنتی را حل كنند. ریاضیات كلید مناسبی برای آمادگی جهت انجام این فعالیتهاست، لذا علوم ریاضی تنها لازمهی كار متخصصان آینده نیست، بلكه جزء لاینفك تعلیم و تربیت عموم مردم به شمار میرود پس ما معلمان وظیفه داریم كه در مورد گسترش و جذابكردن این علم در بین دانشآموزان و حتی مردم تلاش بیشتری انجام داده و به بررسی علل ضعفها و ارائه راهكارهای لازم در این خصوص بپردازیم.
اهداف آموزش ریاضی:
قبل از این كه وارد بحث اصلی شویم یعنی به بررسی علل ضعف آموزشی بپردازیم ابتدا باید هدف از تدریس و آموزش ریاضی را در مدارس مشخص نمایم سپس با توجه به رسیدن به اهداف و دوری و نزدیك آنها ضعفها را مرور كرده و در جهت مشكلات و نواقص راهكارهایی ارائه داد.
از مفهوم آموزش ریاضی نخستین سۆالی كه به ذهن میرسد این است كه چگونه ریاضی را آموزش دهیم؟ هنگامی كه از روش انجام كار صحبت میشود، طبعاً این سۆال پیش میآید كه هدف از انجام این كار چیست سپس در آموزش ریاضی هم باید هدف را مشخص ساخت.
هدفهای آموزش ریاضیات بر حسب سطح فرهنگ ریاضی كه جامعه و محتوای آموزش آن، و در مقاطع تحصیلی مختلف متفاوت بوده و از جامعه به جامعهای دیگر تغییرپذیر است.
ولی منظور اصلی از آموزش ریاضی، عبارت است از: «توسعه قدرت درك و فهم و استدلال، ایجاد طرز فكر صحیح، به وجودآوردن روش استدلال و تفكر منطقی و ایجاد آفرینشهای فكری، در متعلم است»
اهداف آموزش ریاضی به طور كلی به چهار دسته پرورشی، آموزشی، فرهنگی و عاطفی تقسیم میكنند:
الف) هدف پرورش: اهداف پرورشی آموزش ریاضی بدون شك مهمترین بخش اهداف آموزش ریاضی هستند مهم ترین وظیفه آموزش ریاضی تربیت دانشآموز است به نحوی كه بتواند با اتكاء به نفس به مسائل خود بیاندیشد راه چاره پیدا كند و مسایل خود را حل نماید.
ب) هدف آموزش: (با تكنیكهای محاسبهای مورد نیاز دانشآموزان در مدرسه و خارج از مدرسه).
در این هدف باید دانشآموزان را در رابطه با سایر درسها و محاسبات مورد نیاز دروس و نیز محاسبات مربوط به زندگی روزمره آماده ساخت.
ج) هدف فرهنگی: (آشنایی دانشآموز با ریاضی به عنوان بخشی از فرهنگ و اندیشه بشری).
علم ریاضی بخش مهمی از فرهنگ است. اشاره به تاریخ ریاضیات یك ملت میتواند یك احساس غروز و افتخار در ریاضیات را به وجود آورد اعتماد دانشآموزان را بیفزاید و درس را به تاریخ و سنت ملی ربط دهد.
د) هدف عاطفی: لذتی كه میتوان از طریق دنبالكردن فعالیتهای ذهنی و عشقورزیدن به دانشی، به دست آورد ریاضیات ما را متبحر میكند، هم حس كنجكاوی عقلانی و هم حس ظرافت و ادارك را تحریك میكند موریس كلاین میگوید: «ریاضیات عالیترین دستاورد فكری و اصیلترین ابداع ذهن آدمی است»
هدف آموزش ریاضی از دیدگاه جورج پولیا و افلاطون:
از دیدگاه جورج پولیا: مهمترین هدف آموزش ریاضی «اندیشیدن» است و به معلمان توصیه میکند كه باید سطح توانایی و اندیشیدن را در شاگردان خود بالا ببرند.
اهداف آموزش ریاضی به قول افلاطون:
- فرهنگ عمومی،
- قانونمندی فكر،
- عادل به فكركردن،
- رشد فكری و احساس،
- به دستآوردن شخصیت متعادل.
در قرن بیست و یكم هدف اصلی آموزش ریاضی، ایجاد استدلال، حس مسئله ارتباطات و هم چنین تلفیق مقولههای ریاضی و ارتباط آنها با سایر مقولات.
با توجه به اهداف ریاضی كه بیان گردید به این مسئله میرسیم كه چه مشكلاتی و نواقصی وجود دارد كه ما را در رسیدن به اهداف آموزش ریاضی دور میكند و بچهها از این درس شیرین گریزان میكند در ذیل به اهم آ نها خواهیم پرداخت.
عوامل ضعف آموزش ریاضی و مشكلات مربوط به آن:
عوامل ضعف آموزش درس ریاضی كه مربوط به محتوای كتابهای درسی ابتدایی میباشد.
یكی از مهم ترین اهداف آموزش ریاضی در این است كه بچهها بتوانند در شرایط جدید و با توجه به آموختههای قبلی مسایل را حل كنند و این امر وقتی میسر میشود كه با دانشآموزان كار شده باشد و موقعیتهای جدیدی را برای حل مسایل به وجود آوریم با توجه به این مطالب و هدف میبینیم محتوای درسی و كتابهای درسی چه محدودیتهایی را برای معلمان برای رسیدن به این هدف به وجود آورده است.
زمان تدریس ریاضی در مدارس محدود است محتوای ریز مواد درس ریاضی در همه پایهها اول تا پنجم براساس جدول زمانی است اما حل مسئله و تشویق دانشآموزان به فكركردن و پیداكردن روش حل مسئله و انجام تمرینات لازم در این رابطه نیازمند زمان است در دومین همایش ریاضی آقای ایوبیان مقایسه كلاس درس ریاضی معلمان آلمان، ژاپن، آمریكا را با معلم استان كردستان موشكافانه نشان دادند همه دیدیم كه در مدارس كشورهای دیگر معلم مسئلهای میداد و با فراغ بال و خیال آسوده نظارهگر كار دانشآموزان بود ولی معلم استان ما از ثانیه آغازین كلاس درس در جنب و جوش بود متوجه میشویم كه محتوی برنامه درس ریاضی ما طوری طراحی شده كه مفاهیم زیاد تمرینات زیاد را بچهها انجام بدهند بدون اینكه زمانی برای فكركردن برای شاگردان در نظرگرفه شده باشد، سپس معلمان مجبور هستند با توجه به جدول زمانبندی كه حتماً باید 192 صفحه ریاضی پایه سوم در 8 ماه كه یك ماه تعطیلی هم دارد را ارایه دهد پس میبینیم محتوای درسی طوری طراحی شده كه زمانی برای فکرکردن جهت رسیدن به جواب مسئله را برای كودك در نظرنگرفته و هر مطلب درسی در كتاب های ما باید در زمان 45 دقیقه تدریس شود كه این زمان در نرم جهانی فقط برای فكركردن روی مسئله باید به دانشآموز داده شود تا خود به راه حل مسئله برسد.
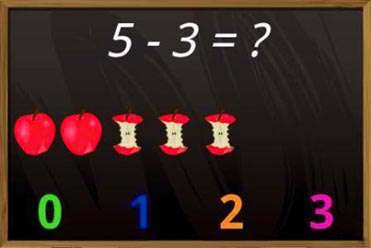
برنامههای كتابهای درس ریاضی در ابتدایی طوری طراحی شده كه هرگونه انتخابی را از معلمان ما سلب كرده كه همین امر باعث شده كه معلمان فقط فكر خود را روی مطالب درسی متمركز كنند در صورتی كه با تجدیدنظر در محتوا و آزاد گذاشتن معلم در انتخاب آن معلم میتواند بین فعالیتهایی كه دانشآموزان را به فكركردن سوق میدهد و فعالیتهای كه فقط مشغول كننده هستند تفاوت بگذارد و فعالیتهایی را كه تسهیلكننده یادگیری در بچهها میشود را انتخاب کند.
برای بیان بهتر این موضوع به كتاب ریاضی پایه چهارم اشاره میكنیم در كتاب ریاضی پایه چهارم دانشآموز در اوج یادگیری و انجام تمرینات تقسیم هستند و كمكم به مرحله حل مسایل مختلف تقسیم نزدیك میشود كه با زدن یك ورق دیگر یك دفعه وارد هندسه و زاویه میشوند و دانش آموز از مطلب تقسیم كنده شده و به مبحث زاویه میپردازد. البته این مشكل ما را بیشتر در ریاضی پایه چهارم میبینیم كه با توجه به بازدید از كلاس حدود 20 نفر از معلم پایه چهارم همه متفقالقول بیان كردند كه مشكل اساسی درس ریاضی در این پایه همین عدم توجه به دستهبندی مطالب درسی میباشد كه پس ارائه یك مطلب و گاهاً در اوج آموزش از مطلب كنده شده و پس از چند صفحه دیگر دوباره به همان بحث میرسند كه دوباره معلم باید آموختههای قبلی را برای بچهها مرور بكند كه این از نظر محدودیت زمان نیز برای معلمان مشكلاتی را فراهم میكند.
4ـ در خصوص عوامل ضعف آموزشی درس ریاضی كه محتوای كتابها موجبات آن را فراهم میكنند:
میتوان گفت توجه به معرفی مشاهیر ریاضی كشور، توجه كم به بازیهای فكری كه كودكان را بیشتر به درس ریاضی جذب كند، به نیازهای اصلی آموزش گیرنده درس توجه كمی شده در این خصوص باید بگویم كه فرد باید نبود چیزی را احساس كند تا نیاز به فكركردن و سپس تلاش در جهت كشف ان را در فرد به وجود آورد، عدم انعطافپذیری برنامهها محتوای درسی در مقابل پیشرفتهای جهانی علم ریاضی را میتوان از دیگر عواملی دانست آموزش این درس را دچار چالش كرده.
عوامل ضعف آموزش ریاضی مربوط به خود دانشآموز ابتدایی
دومین عامل از عوامل ضعف آموزش ریاضی در نظر معلمان از اهمیت ویژه ای برخوردار است علت ضعف در خود كودكان است گاهاً ما دانشآموزانی در مدرسه داریم كه در دروس دیگر نمره قابل قبول میگیرند و در یادگیری مطالب درسی مثل فارسی، تاریخ و. . . موفق هستند اما در درس ریاضی مشكل دارند.
طبق تعریفی كه دیسمور از اختلال ریاضی و حسابكردن كرده است،اختلال در یادگیری ریاضی نارسایی شدیدی است كه در به وجودآمدن مهارتهای حسابكردن و ریاضیات به وجود میآید و با عقبماندگی عاطفی یا عقبماندگی ذهنی و یا شرایط نامساعد مدرسه قابل تبیین است.
به طور كلی نارسایی در یادگیری ریاضی را به دو قسمت تقسیم میكنند:
گاهاً دانشآموزان شكستها و موفقیتهای خود را به چیزهایی نسبت میدهند كه آن ها با این طرز فكر از موفقیتهای خود در درس ریاضی به شانش یا چیز دیگر نسبت میدهند كه به این موضوع درماندگی آموخته شده میگویند كه امروزه متأسفانه درماندگی آموخته شده، در درس ریاضی در بین دانشآموزان بیشتر مشاهده میگردد.
مشكلات روانی از این قبیل باعث به وجودآمدن مشكلاتی در یادگیری درس ریاضی شده كه گریبانگیر دانشآموزان زیادی شده و همین امر ضرورت مشاوران مجرب را در مدارس ابتدایی میطلبد، یكی دیگر از بیمارهای شایع در بین دانشآموزان ترس از اعداد است كه مثل دیگر ترسهای طبیعی نیست و در شرایط معینی بروز میكند با این همه دانشآموزانی كه دچار چنین ترسی شده باشند به
قول پیاژه:
دستخوش نوعی «بیاستعدادنمایی» میشود كه خود به خود درك روابط را دشوار ساخته، مانع یادگیری میشود بنابراین بهجاست اگر مبارزه علیه «ترس از اعداد» را كه اكثریت دانشآموزان را یكباره از اشتغال به مباحث ریاضی روی گردان میكند، از اهم وظایف مدرسه بدانیم.
برش و قسمت:
وقتی می خواهیم یک قطعه یا جسمی رشته مانند را به قسمت های مساوی ویا نامساوی تقسیم کنیم همیشه تعداد قسمتها یکی بیشتر از تعداد برشها است.
مثال: یک آهنگر , میله ای به طول 12 متر را به چهار قسمت تقسیم کرد او برای این کار چند برش زده است؟
برش 3 = 1 – 4 (قسمت)

معلمان بدون آگاهی از روانشناسی، جامعهشناسی روشهای آموزشی، نحوه ارزشیابی و استفاده از وسایل كمك آموزشی، نمیتوانند وظیفه خود را در عصر كنونی به نحو شایسته انجام دهند.
درس ریاضی عموماً برای بچهها مشكل و حتی همراه با ترس و وحشت است. این در حالی است كه ریاضی یكی از چند درسی است كه در باز كردن ذهن دانشآموز و آموزش چگونه اندیشیدن نقش درجه اول دارد. بسیاری از معلمان فرهیخته كه هم به آموزش ریاضی علاقمندند و هم اشتیاق آموختن آن را به بچهها دارند، همواره دنبال راه و روشهایی هستند كه این درس را شیرین و فهمیدنی كنند و در واقع بچهها را با ریاضیات آشتی دهند.
آموزش ریاضی، چند راهکار ساده
بیش از 50 درصد دانشآموزان مقاطع مختلف معمولاً در درس ریاضی مشكلات اساسی دارند. بسیاری از دانشآموزان حتی در سادهترین مطالب ریاضی مربوط به سالهای قبل اشكال دارند. در ابتدای سال تحصیلی معمولاً مشكلات یادگیری ریاضی به دلیل فراموشی مطالب پایه بسیار زیاد است و دانشآموزان كشش لازم برای یادگیری ریاضی را ندارند و وقتی كه مطالبی را تدریس میكنیم نمیفهمند و با دهان باز و چشمانی گرد شده به معلم و تخته سیاه مینگرند! وقتی كه از چند نفرشان درس میپرسیم به ندرت كسی جواب درستی میدهد و دائم هراسناك بوده و چشمانشان را به زمین میدوزند! اگر یك امتحان پایه از آن ها بگیریم میانگین نمرات امتحانی پایین خواهد بود. علل بسیاری در پایین بودن نمرات امتحانی نقش دارند.
از جمله آن ها:
1ـ پایه ضعیف در درس ریاضی از سالهای قبل.
2ـ قبولی با استفاده از تكماده در خرداد سال قبل.
3ـ قبولی با استفاده از تقلب و گفته شدن سوالات قبل از امتحانات.
4ـ كمهوشی و دیرآموزی بعضی از دانشآموزان.
5 ـ نداشتن اعتماد به نفس در درس ریاضی.
6 ـ مشكلات جسمی بعضی از دانشآموزان، سوء تغذیه، ضعف چشم.

اقدامهایی كه برای چنین دانشآموزانی میتوان انجام داد به قرار زیر است:
ابتدا باید در چند جلسه اعتماد به نفس دانشآموزان را تقویت كرد. برگزاری امتحانات به صورت كتاب باز (open book) میتواند انجام شود تا دانشآموزان اعتماد به نفس پیدا كنند.
باید آن ها را تشویق كرد كه خودشان مطالب را یاد بگیرند و تمرینها را حل كنند و زود نا امید نشوند. اگر دانشآموزی تمرینی را حتی ناقص حل كند، باید او را تشویق كرد و نمرات بیش از حقش به او داد. هر بار كه با كوچكترین مطلبی یك نمره خوب برای دانشآموز گذاشته شود، كمكم این دانشآموز از درس ریاضی و معلم ریاضی خوشش میآید. باید سعی كرد ضعفهای دانشآموز را به رویش نیاورد.
با هم مطالعه كردن یكی از روشهای شناخته شده و موثر یادگیری در میان دانشآموزان است. پژوهشهایی كه درباره اثربخشی از روش مطالعه مشاركتی انجام گرفته است نشان دادهاند، دانشآموزان و دانشجویانی كه به این طریق مطالعه میكنند، از كسانی كه مطالب را برای خودشان خلاصه میكنند یا صرفاً به مطالعه مطالب میپردازند، بیشتر میآموزند و آموختهها را برای مدت طولانیتری در یاد نگه میدارند.
به همین جهت گروهبندی دانشآموزان در كلاس كه متشكل از دانشآموزان ضعیف و قوی و متوسط باشد، در رفع اشكالات درسی آنان بسیار موثر است. نوشتن چركنویس هم در بسیاری از دانشآموزان كمككننده است. تمرین و تكرار در زمان های متفاوت هم در به خاطرسپاری و یادگیری مطالب ریاضی نقشی اساسی دارند كه معمولاً دانشآموزان ضعیف از آن غافل هستند.
البته میتوان از راههای مختلف دیگر به یادگیری ریاضی در سطح مدارس كمك كرد كه عبارتند از:
الف: ایجاد امكانات لازم برای افزایش سطح فرهنگی خانواده كه بتواند بسیاری از مشكلات درسی فرزند خود را برطرف كند.
ب: آموزش روشهای جدید تدریس به معلمان و حذف روشهای سنتی.
ج: تهیه وسایل كمك آموزشی در زمینه تدریس.
و: طرح درس معلم.

اگر معلم برای خود طرح درس داشته باشد یعنی یقیناً بداند كه در هر جلسه چه مطالبی میخواهد درس بدهد و این موضوع چه مشكلاتی دارد و در ضمن سعی كند كه با استفاده از تجربیات گذشته در حداقل زمان و كمترین كلام، حق درس را ادا نماید. نخستین گام این است كه دبیر تعداد صفحات كتاب را به تعداد جلسات مفید نوبت یا سال تقسیم كند و ببیند در یك جلسه دقیقاً چند صفحه باید تدریس كند و اگر لازم شد ابزار و وسایل كمكآموزشی از قبل تهیه شده را به كلاس برده و مورد استفاده قرار گیرد.
قسمتی از همكاری و همیاری بچهها در خارج از كلاس یا در منزل صورت پذیرد. مثلاً بچهها در منزل اشكالی را روی مقوا بكشند یا اجسامی بسازند یا اشكالی ببرند یا جدولهایی را تنظیم كنند منتهی با پرسش و سوال در كلاس دانشآموز را فعال كرد.
باید توجه داشت تا زمانی كه معلم رو به تابلو و پشت به بچهها تندتند فرمول نوشته، تخته را سیاه كرده و پاك كند و در آخر درس رو به كلاس برگر دانده و بگوید: بچهها درس برای روز بعد از فلان صفحه تمرین حل كنید. همواره بچهها در ریاضی ضعیف خواهند ماند. تا زمانی كه معلمان ریاضی مخصوصاً در مقاطع ابتدایی هنوز از روشهای قدیمی حفظی برای تدریس ریاضی استفاده میكنند، بیشتر دانشآموزان ابتدایی از ریاضی گریزان خواهند شد.
كلاس درس ریاضی برای برخی دانش آموزان ازجمله كلاسهایی است كه معادلات و مفاهیم آن سخت است و دیر تمام میشود و حضور در این كلاسها برای این دانشآموزان جذابیت لازم را ندارد.

اینكه چرا برخی دانش آموزان با درس ریاضی مشکل دارند؟ موضوعی است كه درباره آن با استادان دانشگاه و نخبگان گفتگو کردهایم.
دکتر آرش رستگار، عضو هیئت علمی دانشگاه صنعتی شریف میگوید:"چون ریاضی مطابق با سبک یادگیری دانش آموزان آموزش داده نمیشود به صورت درسی سخت خود را نشان میدهد در صورتی که اگر این قاعده رعایت شود به درسی آسان تبدیل خواهد شد.
وی با بیان اینکه شیوه آموزشی این درس باید چنان باشد که به همه دانش آموزان در بعد کاربرد و رشد ساختار شناختی کمک کند ادامه میدهد: "ریاضیات را با انجام دادن میتوان یاد گرفت."
علی رضا زارعی، عضو هیئت علمی دانشگاه شریف نیز میگوید:"ریاضی مانند سایر دروس برای برخی از دانشجویان یا دانش آموزان سخت است و این سختی در تفاوت ساختار این درس با سایر دروس است چرا که درس ریاضی استعدادهای خاص خود را میطلبد."
وی به نقش ویژه آموزش در این زمینه اشاره میکند و میگوید:"شیوه آموزشی باید از طریق تحریک علایق افراد و ایجاد ارتباط بین این علایق به درس ریاضی ایجاد شود."
روح الله مهکام دارای مدال طلای ریاضی و دانش آموخته دانشگاه شریف هم اضافه میکند: "ریاضی درس آسانی نیست ولی عامل اصلی بیعلاقه بودن دانش آموزان به این درس پایه ضعیف آنهاست که چون درسهای سال قبل را خوب یاد نگرفتهاند با مشکل مواجه میشوند.
ناگفته پیداست که شیوه درست آموزش یکی از روشهای علاقهمند کردن بچهها به ریاضی است و از دانش آموزان خواست از فکر کردن بر مسائلی که در مواجه با آنها احساس عدم توانایی میکنند نهراسند."

به گفته عرفان صلواتی از دانشجویان دکتری دانشگاه صنعتی شریف، ریاضی مانند دیگر دروس اگر به طور درست و مستمر خوانده شود درس سختی نیست و اینکه بسیاری از دانش آموزان علاقهای به درس ریاضی ندارند درست و علمی نیست.
وی ادامه میدهد:"یکی از خصوصیاتی که در درس ریاضی وجود دارد لازمه یادگیری یک مطلب مستلزم تسلط بر درسهای سال قبل است و توصیه من این است که دانش آموزان اگر احساس میکنند مطلبی را یاد نگرفتهاند به دروس سالهای فبل مراجعه کنند."
این نخبه علمی تصریح میکند که نقش معلمان در یادگیری بسیار مهم است و باید این درس را برای دانش آموزان ملموس و قابل دسترسی کنند.
سید حسام فیروزی، دانشجوی دانشگاه صنعتی شریف هم اضافه میکند:"ریاضی هم سخت است و هم آسان است. آسان است زیرا همه ساختار آن منطقی و متقن است، اما قدری هم سخت است زیرا فهمیدن ساختارهای منطقی به تفکر نیاز دارد و فکر کردن عمیق قدری برای برخی افراد سخت است بخش مهمی از بیعلاقگی دانش آموزان به دلیل نحوه نامناسب آموزش ریاضی است."

در فایل زیر که به صورت فلش تهیه شده شما با اندازه گیری زاویه بوسیله ی نقاله آشنا خواهید شد. با پاسخ دادن به 10 سوالی که از شما پرسیده می شود می توانید بهتر از قبل کار با نقاله را یاد بگیرید. میزان خطای پاسخ شما توسط کامپیوتر نشان داده خواهد شد. پس سعی کنید خطاهای اندازه گیری خود را به صفر برسانید. همین حالا تمرین کنید .
انیمیشن دو خط موازی و یک خط مورب
عمده ترین روش های حل مساله ریاضی
جستجو برای الگو
رسم شکل
صورت بندی مساله معادل تغییر مساله
انتخاب نمادهای مناسب
استفاده از تقارن
تجزیه به حالت های ساده تر
کار عقب رونده
بررسی نقیض
زوجیت
بررسی حالتهای حدی
تعمیم
عمده ترین روش های حل مساله ریاضی
۱) جستجو برای الگو:
همواره کار حل مساله را با نوعی ادراک شهودی از مساله شروع می کنیم و با بررسی چند حالت خاص به سوی الگوسازی برای حل کامل آن جلو می رویم.
۲) رسم شکل:
در هر مساله ای که امکانپذیر باشد رسم یک شکل (اعم از هندسی یا یک نمودار و غیره) می تواند در یافتن حل مساله الهام بخش باشد و رابطه بین اجزا مساله را بهتر نمایان می سازد.
۳) صورت بندی مساله معادل:
در بخش قبل دیدیم که گام نخست در حل مساله عبارت است از جمع آوری داده - جستجو - فهمیدن مساله - برقراری ارتباط بین اجزا - حدس زدن و تجزیه تحلیل. ولی اگر همه این کارها به روش معقولی میسر نباشد چه کنیم؟ یعنی اینکه ممکن است کارهای محاسباتی خیلی پیچیده باشد و یا به سادگی نتوانیم حالتهای خاصی را مطرح کنیم تا به بینش لازم برسیم.آنچه در چنین شرایطی توصیه می شود این است که مساله را با مساله ای معادل ولی ساده تر جایگزین کنیم. راه کلی در این گونه معادل سازی به بینش و تجربه های عمومی باز می گردد ولی کارهایی از قبیل دستکاریهای جبری یا مثلثاتی و تفسیر مجدد مساله با زبانی دیگر می تواند موثر باشد.
۴) تغییر مساله:
در بعضی مسائل می توانیم مساله مورد نظر را به مساله دیگری تبدیل کنیم. این دو مساله لزوما معادل یکدیگر نیستند ولی حل مساله دوم حل مساله اول را نتیجه می دهد.
۵) انتخاب نمادهای مناسب:
از نخستین گام ها در حل مساله های ریاضی تبدیل مساله به صورتی نمادین می باشد. در انتخاب نمادها باید هر ایده کلی را ملحوظ داشته و آن را با نمادی بیان کنیم. بی دقتی در انتخاب نمادها ممکن است به از بین رفتن یا مبهم شدن بعضی از روابط منجر شود.
۶) استفاده از تقارن:
وجود تقارن در یک مساله موجب می شود که با عملیات کمتری مساله را به جواب برسانیم.
۷) تجزیه به حالت های ساده تر:
گاهی اوقات می توان یک مساله را به تعدادی مساله ساده تر و کوچکتر تبدیل کرد که هر کدام از این مسائل ساده تر را می توان جداگانه در نظر گرفت.
۸) کار عقب رونده:
کار عقب رونده یعنی اینکه نتیجه مورد نظر را مفروض گرفته شروع به استنتاج هایی از آن کنیم تا به یک مساله حل شده برسیم. در این صورت گامهای معکوسی را در نظر بگیریم تا به نتیجه مطلوب دست پیدا کنیم.
۹) بررسی نقیض:
استفاده از تناقض یعنی مفروض گرفتن نادرستی حکم و با استنتاج به نتیجه نادرست یا متناقضی رسیدن از روشهای آشنا در ریاضیات است.
۱۰) زوجیت:
ایده ساده زوج و فرد بودن یکی از ابزارهای بسیار قوی در حل مساله است که کاربردهای وسیعی دارد.
۱۱) بررسی حالت های حدی:
در برخورد اولیه با مساله بعضی اوقات تغییردادن پارامترها بین حدهای پایین و بالای ممکن آنها ایده هایی برای حل مساله به همراه خواهد داشت.
۱۲) تعمیم:
معمولا ساده سازی یک مساله راهگشای حل آن است. اما در بعضی موارد حالت تعمیم یافته مساله سهل تر قابل حل است و حالت مورد نظر را می توان به عنوان یک حالت خاص نتیجه گرفت. در واقع ایده تعمیم و در کنار آن مجرد سازی ویژگی خاص ریاضیات نوین است.
در پایان اشاره می کنم که سعی کنید یک مساله را در صورت امکان به چند روش حل کنید. این کار باعث بهبود سرعت و خلاقیت شما در حل مسائل دیگر می شود. روش های مختلف حل مساله بخش هایی از زوایای پنهان مساله را برای شما آشکار می کند.
ویژگی های ریاضیات
- اولین ویژگی ریاضیات دقت است، کم و زیاد شدن یک صفر ، مثبت یا منفی در نظر گرفتن یک رقم ، پس و پیش کردن یک نماد ، اضافه کردن یک کلمه و ... هر کدام میتواند مسالهای را به جوابی دیگر رساند یا صورت مساله را عوض کند.
- دومین ویژگی ریاضیات ، خلاصه گویی و استفاده از مطالب ، قضیهها و مسالههای اثبات شده به عنوان ابزارهایی برای حل مسالههای جدید است و این که همواره به دنبال دادههای صحیح و کوتاه باشیم.
جنبههای مختلف ریاضیات
ریاضیات به عنوان یک ابزار
یعنی وسیلهای برای توصیف و تجزیه و تحلیل و انتقال آن ، به دلیل گنگ و نامفهوم بودن زبانهای معمولی.
ریاضیات به عنوان یک موضوع
ریاضیات علاقه میآفریند و لذت میبخشد و ارزش مطالعه محض و مستقل از کاربرد دارد که خود جنبه آزادی اندیشه را از قید زمان و مکان میطلبد چرا که در بسیاری از موارد مطالعات در خارج از فضای سه بعدی و در فضاهای آفریده شده توسط ریاضیدان صورت میگیرد. بطوری که بیشتر مفاهیم مهم ریاضی به واسطه همین ، امروز کاربرد زیادی پیدا کردهاند. همان طور که در ساختن بدن سالم نیاز به ورزش مکرر فیزیکی داریم.
ریاضیات به عنوان یک علم
یعنی از دیدگاه کاربردی که نقش و ارزش آن در جوامع کنونی بشری روز به روز مورد توجه قرار گرفته است و کاملا محسوس میباشد.
ریاضیات به عنوان یک مساله تربیتی
برای پرورش ونظم فکری و بالابردن قدرت اندیشه و استدلال منطقی همچنین رشد قوه خلاقیت ذهنی که شاید این جنبه از ریاضیات مهمترین هدف از تدریس آن میباشد.
ریاضیات از دیدگاه دانشمندان
- گالیله میگوید: اصول ریاضیات الفبای زبانی است که خداوند جهان را با آن نوشته است و بدون کمک آنها درک یک کلمه هم غیر ممکن است. و انسان بیهوده در راهروهای تاریک و پر پیچ و خم سرگردان است.
- لئوناردو داوینچی معتقد است که: هیچ دانشی را نمیتوان دانش واقعی دانست مگر این که به صورت ریاضیات متجلی شود.
- واجر بیکن معتقد است که: ریاضیات دروازه علوم است غفلت از ریاضیات به همه دانشها لطمه میزند زیرا کسی که علوم دیگر را نمیتواند درک کند و اشیای دیگر جهان را نمیشناسد. و بدتر از آن کسانی که نادانند نمیتوانند جهالت خود را درک کنند.
- کانت میگوید: در هر بخش از علوم فیزیکی به معنای عام آن قدر از علم واقعی است که در آن ریاضیات وجود دارد یعنی علوم منهای ریاضیات یعنی هیچ.
فرجام سخن
بنابراین اگرفردی به هر دلیل در رسیدن به هدف از ریاضی کمک نگیرد، وظیفه خود را انجام نداده است و همچنین اگر شخصی توانایی را در این مورد بدست نیاورد نه تنها توفیقی به دست نمیآورد، بلکه در زندگی اجتماعی نیز از طریق راههای سالم پیروزی چشمگیر نخواهد داشت. میتوان نتیجه گرفت که ریاضیات غذای مغز است. که باید بطور حساب شده به مغز برسد. همچنین ریاضیات مانند غلتکی است که جاده ناهموار و سنگلاخ علم را صاف و هموار میسازد تا دیگر علوم در گذر زمان سرعت بیشتری بگیرند.
.: Weblog Themes By Pichak :.





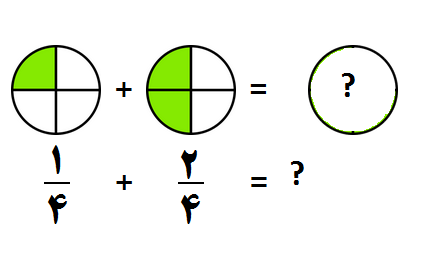
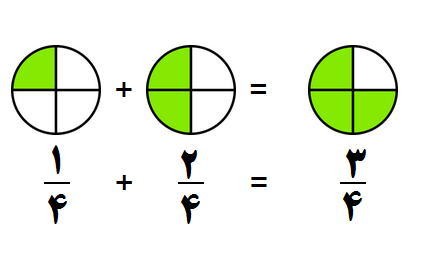
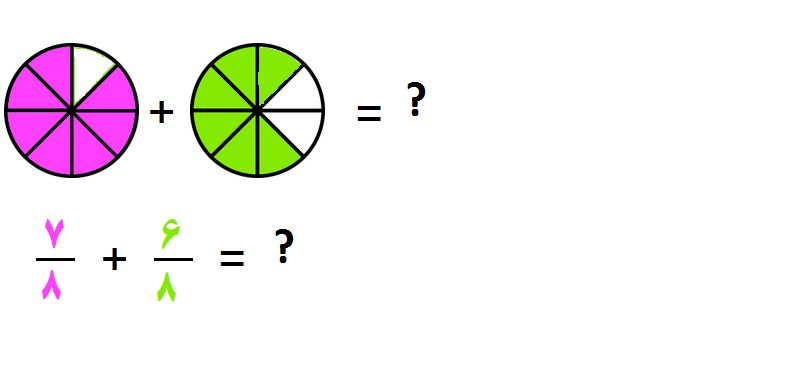
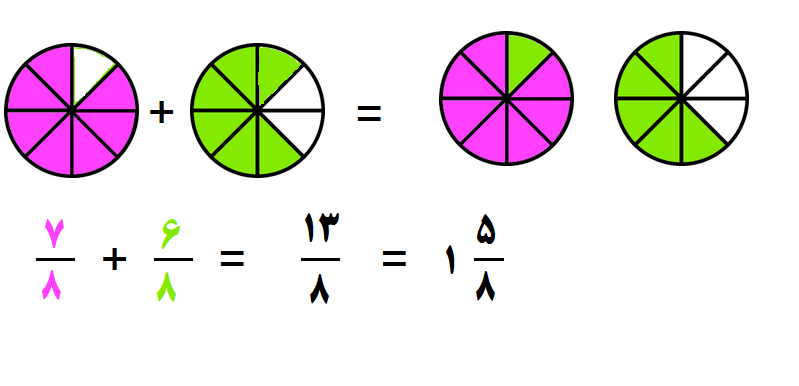
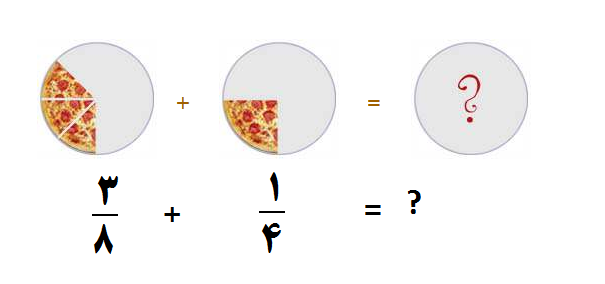
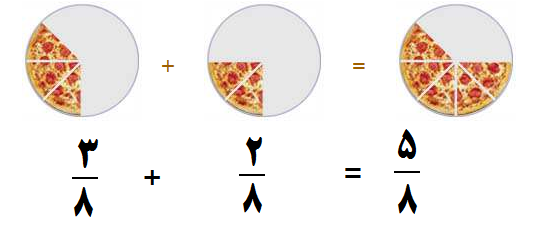


















































 آمار
وب سایت:
آمار
وب سایت:

