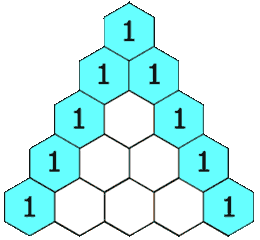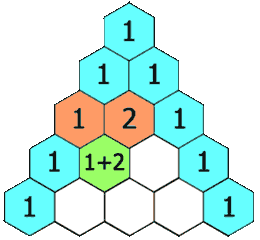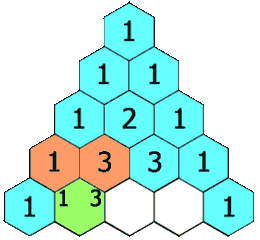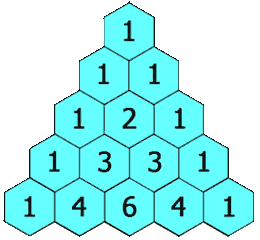
ا این بیت شعر شما میتوانید عدد پی را تا ده رقم اعشار به خاطر بسپارید...
خرد و دانش و آگاهی دانشمندان ره سرمنزل مقصود بما آموزد
تعداد حروف هر کلمه نشان دهندهی یک رقم از عدد پی است.
تعداد حروف خرد=3
تعداد حروف و = 1
تعداد حروف دانش = 4
.
.
.
3/1415926535= عدد پی تا ده رقم اعشار
عدد گنگ پی
یکی از اعداد ویژه ریاضی است که قرن ها ریاضیدانان را به خود مشغول نموده است. این عدد که حاصل تقسیم محیط یک دایره بر طول قطر آن می باشد عددی است متعالی به عبارت دیگر قابل ترسیم نیست. عدد پی تا ۱۰۰۰ رقم اعشار به صورت زیر است:
3.1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989
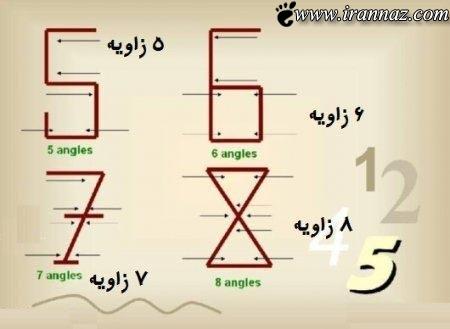
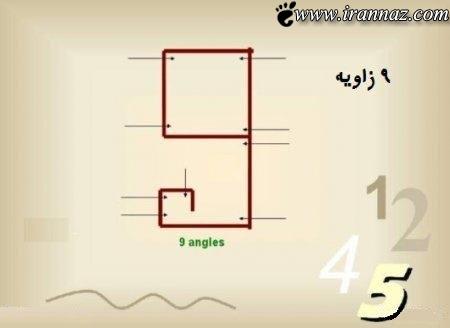
صفر بدون زاویه

۱- ضرب اعداد بین ۱۰ تا ۲۰ در هم :
فرض ۱۹ و ۱۷
۱- عدد بزرگتر رو با یکان عدد کوچکتر جمع کن! ( ۲۶ = ۷ + ۱۹ )
۲- یه صفر سمت راست عددی که به دست آوردی اضافه کن ( ضربدر ۱۰ کن ) ( ۲۶۰ )
۳- عدد حاصل رو با حاصل ضرب یکان های ۲ عدد جمع کن. ( ۳۲۳ = ( ۷ * ۹ ) + ۲۶۰ )
۲- ضرب عدد ۱۱ در اعداد ۲ رقمی :
فرض ۱۱ و ۸۱ را در هم ضرب کنیم :
۱- مجموع ارقام اون عدد رو بدست بیار. ( ۹ = ۱ + ۸ )
۲- عددی که بدست آوردی رو بذار بین عددت! ( ۸۹۱ )
۳- این روش کوچکترین فرقی با روش عادی نداره ولی سریعتره
در ضمن اگه حاصل جمع ارقام عددت از ۱۰ بیشتر شد، فقط یکان حاصل جمع رو بذار وسط و به صدگان ۱ واحد اضافه کن!
مثلاً برای ضرب ۹۳ در عدد ۱۱ داریم :
۱- ۱۲ = ۳ + ۹
۲- ۳(۱۲)۹ ——-> 1023
3- توان دوم اعداد ۲ رقمی منتهی به ۵ :
فرض عدد ۸۵ را به توان ۲ می رسانیم :
۱- دهگان عددتو با یکی بیشتر از خودش ضرب کن ( ۷۲ = ۹ * ۸ )
۲- یه ۲۵ بذار جلوش! ( ۷۲۲۵ )
ضربهای ذهنی و ترفند های آن
بااین ترفند ، قادر خواهید بود هر دو عددی ، از 11 تا 19 را بدون استفاده از ماشین حساب، بسرعت در ذهن خود ضرب کنید. در این جا به طور مثال
19×16 را آزمایش می کنیم.
عملیات : عدد بزرگتر را با یکان عدد کوچکتر جمع کنید .
یعنی 25 = 6+19 و در جلوی حاصل جمع صفر قراردهید (250 ) . سپس یکان دو عد را در هم ضرب کنید و با عدد قبلی جمع کنید . یعنی 54 = 6 × 9 و 304 = 54+250 جواب ما 304 است .
اگر این عمل را چند بار تکرار کنید به راحتی و در دو سه ثانیه می تونید ضرب های دورقمی زیر 20 رو حل کنید.
----------------------------------------------------------------------------------
یه روش دیگه هم هست ... یکان ها رو با هم جمع کنید و ضربدر 10 کنید و با ضرب یکان ها جمع کنید و در نهایت بعلاوه ی 100 کنید !!
اینطوری برای اعداد بین 20 و 30 یا بین 30 و 40 یا .... هم میشه تعمیم داد !
مثلا برای 20 تا 30 ... یکان ها را با هم جمع کنید و ضربدر 20 کنید و با ضرب یکان ها جمع کنید و در نهایت بعلاوه ی 400 کنید ! البته ضربدر 20 کردن یکم سخت تر میشه ... مخصوصا بیشتر از 30...
------------------------------------------------------------------------------------------------------
ضرب جادویی
عدد9 واز آنجا که یکی از اعداد بزرگ ومشکل جدول ضرب است میتوانیم از انگشتان دست کمک بگیریم بطور مثال برای ضرب 4 در9 به این صورت عمل میکنیم که: هر10 انگشت دو دست را باز کرده ورو به بچه ها میگوییم بچه ها 9 درچه عددی ضرب شده؟ پاسخ:4 پس از دست چپ وسمت چپ انگشت چهارم را بسته وانگشتان قبل از انگشت بسته را ده تایی وبعد از آنرا یکی حساب میکنیم که در اینجا 3ده تایی و6یکی خواهیم داشت که پاسخ 9در4 است که می شود 36.
امتحان کنید ضرب عددهای یک رقمی دیگری را در 9 به این روش محاسبه کنید برای دانش آموزان جالب خواهد بود.
------------------------------------------------------------------------------------------
عدد 37
عدد 37 را در اعداد 3-6-9-12-15-18-21 (مضربهای 3)ضرب کنیم جواب یک عدد سه رقمی خواهد بود که 3 رقم ان تکرار میشود.
333=9×37 666= 37×18 777 = 37×21 444 = 12×37
------------------------------------------------------------------------------------------------------------
پیداکردن شماره خانه وسن هر شخص
1-از او بخواهید شماره منزلی را در نظر بگیرد وانرا دو برابر کند.2-به حاصل عدد 5را اضافه کنید.3-در 50 ضرب کنید.4-سنش را به حاصل اضافه کنید 5-شماره روزهای سال(365)را به حاصل اضافه کنید. 6- 615 را از جواب کم کنید.7-ارقام عدد حاصل از راست،سن شخص وبقیه شماره منزل او خواهد بود.
---------------------------------------------------------------------------------------------------------------------
خواندن فکر دیگران
دوست شما یک عدد دو رقمی بین 1و9 انتخاب میکند و به ذهن میسپارد،مثلا 7و3-یکی از دو عدد را در 5 ضرب میکنیم 15=5×3 –عدد 3 را به حاصل ضرب می افزاییم 18=3+15-حاصل جمع را دو برابر می کنیم 36=2×18-حاصل را با عدد دیگری که انتخاب کرده بودید جمع کنید 43=7+36-حاصل را به شما بگوید سپس شما عدد 6 را از حاصل کم کنید.37=6-43_(عدد بدست امده از اعداد انتخاب شده تشکیل شده است
آموزش جدول ضرب با استفاده از خطوط متقاطع
مثال :
ضرب 20= 4* 5
برای ضرب 4*5 ابتدا 5 عدد خط افقی می کشیم بعد 4 خط عمودی طوری می کشیم که خطوط افقی را قطع کند بعد نقاط متقاطع را با نقطه مشخص نموده و می شماریم که نقطه های مورد نظر 20 تا خواهد شد . برای ضرب های یک رقمی در یک رقمی کاربرد دارند.
ضرب هایی مانند 25*25
برای ضرب هایی مانند 25*25 به صورت ستونی زیر هم می نویسیم ابتدا یکی ها را در هم ضرب می کنیم که میشود 25 را زیر یکی ها نوشته بعد یکی به 2 در ده تایی ها اضافه می کنیم که می شود 3 بعد 2 را در 3 ضرب می کنیم جواب خواهد شد 625 25*25= 625
برای ضرب هایی مانند 35*35 و غیره همین طور عمل می کنیم .
عدد اول را با یکان عدد دوم (فرقی نمیکنه کدام اول و کدام دوم باشه )جمع و حاصل را ضربدر دهگان می کنیم و حاصلو با حاصل ضرب یکان دو عدد جمع می کنیم 14*18 14+8=22*10=220+32=252 18*19 18+9=270*10=270+72=342 35*37 35+7=42×30=1260+35=1292 برای اینکه بتونید سریع این ضربو انجام بدین حتما چند بار تکرارکنید
ضرب دو عدد دو رقمی مساوی که رقم یکان 5 داشته باشد به این صورت است که حاصل به 25 ختم خواهد شدو رقم بعدی از حاصل ضرب دهگان در یکی بیشتر از دهگان خواهد بود. مثال: 35×35= 3×4=12 1225 85×85=7225 8×9=72 75×75=5625 7×8=56
![]()
| مرکز تحقيقات فيزيک و رياضيات نظري | |
| گروه ریاضی دانشگاه شريف | رياضيات دانشگاه شريف |
| گروه ریاضی دانشگاه تهران | دانشگاه تهران |
|
سایتی دارای سوالات المپیاد ریاضی 98 همراه با جواب آن ها |
|
|
انجمن ریاضی ایران مکانی برای اعلام کنفرانس ها و مسابقات ریاضی و خبرهای آن و نیز اطلاعاتی از ریاضیات |
|
| دارای مطالب و سوال و جواب های ریاضی schoolnet باشگاه ریاضی در سایت | |
| اولين مجله الكترونيكي رياضي در ايران | لبخند رياضي |
| مرجعی برای علاقه مندان به ریاضی | riazicenter |
| المپیاد ریاضی ایران | المپیاد ریاضی ایران |
| ریاضی دبیرستان | ریاضی دبیرستان |
| وبلاگ های ایرانی | |
| سوال و جواب ریاضی | |
| آموزش ریاضی و آمار و احتمالات | |
| يادداشت هاي يك معلم رياضي | زنگ رياضی |
| مطالب زیبای ریاضی و فیزیک | ????? |
| ما همه عاشق ریاضی هستیم | ما عاشق رياضی هستي |
| وبلاگ گروهي معامان رياضي راهنمايي كشور - چيزي شبيه به اهداف كلاس هاي ضمن خدمت | وبلاگ گروهی معلمان ریاضی |
|
ریاضی... ریاضیات... علم و دانش... تحقیق و بررسی... |
گروه رياضيات آحو |
| اين سايت به آموزش رياضيات از ابتدايي تا دانشگاه مي پردازد | ستارگان رياضي 83 |
| بينهايت و تكنيك هاي اثبات قضايا | بینهايت |
| جذابیت ها ی ریاضی و معماهاي رياضي | جذابيتهای رياضی |
| وبلاگ دانشجوي رياضيات محض، حاوي مقالات و خبرهاي دنياي رياضيات | جهان رياضی |
| ریاضیات عالی و معاصر | رياضيات زيبا |
| رياضي نمونه سوال و پرسش هایی از ریاضیات دبیرستانی | رياضيات دبيرستانی |
| تاريخچه و مطالب رياضي | رياضيات قانون ذهن |
| طرح و ارائه مسائل ریاضیات | رياضيات و سرگرمی |
| دانشجوی ریاضی محض دانشگاه صنعتی امیرکبیر | رياضی برای همه |
| این وبلاگ مختص تمام عاشقان ریاضی میباشد. | رياضی شيرينی زندگانی |
| انجمن ریاضی دبیرستان علامه طباطبایی | رياضی عشق من |
| ریاضیات کاربردی و علوم کامپیوتر | رياضی کاربردی |
| رياضيات سرشار از زيباي | ریاضیات سرشار از زیبایی |
| مطالبی در رابطه با کاربرد آمار در انتخاب استراتژی و تصمیم سازی | |
|
وبلاگی در مورد زیبایی های ریاضی ، کاربرد ریاضی در جامعه و آموزش ریاضی |
یک نگاه کشاف گستاخ |
| آموزش و پژوهش در زمینه ریاضیات | اميد رياضی |
| مطالب ریاضی مختلف | اويلر رياضيدان |
| برخال معادل فارسی فراکتال است شاخه ای از هندسه كه به مطالعه اشكال پيچيده در طبيعت مي پردازد | برخال و طبيعت |
| مقالات آموزشي رياضي | به دنیایریاضیات خوشآمدی |
|
مطالب وآموزش هایی در زمینه ریاضیات و نیز راه های های آموزش ریاضی |
|
|
وبلاگی متعلق به یک دانشجوی رشته ریاضیات محض، حاوی مطالبی در زمینه ریاضیات |
|
|
مطالبی در زمینه ریاضیات و دانشمندان ریاضی و اعلام کنفرانس ها و نیز مطالبی درباره نحوه آموزش ریاضیات |
|
| آموزش ریاضی دبیرستان - توابع حسابی و عددی | |
|
وبلاگی در زمینه روش های مختلف محاسبات ریاضی |
|
| متروید - شاخه ای از ریاضیات عالی | متروید |
| ریاضیات مقدماتی و تخصصی | ریاضیات مقدماتی و تخصصی |
| سایت های انگلیسی | |
| جامعه رياضيات آمريكا | |
| ریاضی دانشگاه هاروارد | ریاضی دانشگاه هاروارد |
| انجمن رياضيات دانشگاه آكسفورد | انجمن رياضيات دانشگاه آكسفورد |
| معماهاي رياضي | معماهاي رياضي |
| اطلاعات شغلی ریاضی | اطلاعات شغلی ریاضی |
| RICE مرکز رياضيات دانشگاه | http://math.rice.edu |
| رياضيات ايالت اوكلاهاما | www.math.okstate.edu |
| استادان رياضي و علوم کامپيوتر | www.wisdom.weizmann.ac.il |
| مركز رياضيات دانشگاه واشينگتن | www.math.washington.edu |
| Linz کاربرد گروهي جبر در | www.algebra.uni-linz.ac.at |
| رياضيات و آمار | www.math.mun.ca |
| دانشگاه هاروارد | ath.harvard.edu |
| اطلاعات شغلي رياضيات | www.mathjobs.org/jobs |
| هندسه | www.cs.elte.hu/geometry |
| آزمايشگاه رياضيات | www.cecm.sfu.ca |
| Minnesota مرکز رياضيات | www.math.umn.edu |
| سيستم کنترل و ديناميک | www.cds.caltech.edu |
| انجمن سخت کوشي رياضي | www.math.ntnu.no |
| بزرگترین سایت منابع ریاضی در وب - انگلیسی | جهان ریاضی |
| اطلس ریاضی - درگاهی به ریاضیات مدرن - انگلیسی | اطلس ریاضی |
| كاربرد كامپيوتر و اينترنت در رياضي | |
| institute for studies in theoritical physics and mathematics - مدرسه ریاضیات | |
| آخرین خبرها و رخدادهای عالم ریاضی | msri |
| mathematics department of MIT college دسترسی به مواد درسی ریاضیات دانشگاه |
|
| بيوگرافي رياضيدانان جهان | |
| شامل مقالات آموزشي در زمينه هاي Number Theory, Combinatorics, Geometry, Algebra, Calculus & Diff Eqs, Probability & Statistics, Set Theory & Foundations |
|
| آمار | |
| آموزش ریاضی و آمار و احتمالات | |
| پژوهشكده آمار | |
چند ضلعی (polygon) : به شکل دو بعدی در صفحه که با مسیری بسته شامل تعداد متناهی خطوط راست محیط شده باشند، چند ضلعی گفته می شود.
چند ضلعی ها به دو دسته اصلی ساده و خود متقاطع(پیچیده) تقسیم می شوند.
-
- چند ضلعی ساده (simple) : چند ضلعی که اضلاع آن یکدیگر را قطع نمی کنند، مگر در راس ها که دو ضلع به هم می رسند. چند ضلعی های ساده به دو دسته محدب (کوژ) و مقعر (کاو) تقسیم می شوند.
چند ضلعی محدب (convex) : چند ضلعی که از هر دو نقطه دلخواه درون آن پاره خطی به هم وصل کنیم ، آن پاره خط از داخل چند ضلعی عبورمی کند. یا به عبارت دیگر چند ضلعی که هیچ یک از زاویه های آن بیشتر از 180 درجه نباشد.
چند ضلعی مقعر (concave) : به چند ضلعی های غیر محدب ساده چند ضلعی مقعر می گویند یا به عبارت دیگر چند ضلعی های ساده ای که زاویه بیش از 180 درجه داشته باشند مقعر گفته می شود.
چند ضلعی نامحدب (non-convex) : چند ضلعی که دو نقطه درون آن بیابیم که پاره خط واصل این دو نقطه در خارج از چند ضلعی عبور کند ، یک چند ضلعی نامحدب می باشد.(دقت کنید که یک چند ضلعی نا محدب هم می تواند ساده باشد و هم خود متقاطع )
-
 چند ضلعی خود متقاطع یا پیچیده (self-intersecting or complex) : اضلاع چند ضلعی یکدیگر را در محلی غیر از راس ها قطع می کنند . این محل های تقاطع راس به حساب نمی آیند.
چند ضلعی خود متقاطع یا پیچیده (self-intersecting or complex) : اضلاع چند ضلعی یکدیگر را در محلی غیر از راس ها قطع می کنند . این محل های تقاطع راس به حساب نمی آیند.
- چند ضلعی های ستاره ای (star polygon) : چند ضلعی های متقاطع که دارای اضلاع متساوی هستند.
- چند ضلعی های متساوی الاضلاع (Equilateral) : چند ضلعی هایی که اضلاع متساوی دارند. (چند ضلعی های نامحدب متساوی الاضلاع 5 یا بیش از 5 ضلع دارند.)
- چند ضلعی های متساوی الزوایا (Equiangular) : تمام زوایای داخلی راس ها با هم برابرند.
- چند ضلعی های محاطی (cyclic) : راس ها بر روی محیط یک دایره واحد قرار دارند.(دایره محیطی نامیده می شود.)
- چند ضلعی محیطی یا مماسی (Tangential) : همه اضلاع بر دایره محاطی مماس اند.
- چند ضلعی های منتظم (Regular) : چهار ضلعی محاطی که متساوی الاضلاع باشد منتظم است. به عبارت دیگر چند ضلعی که اضلاع آن با هم و زاویه های آن با هم برابرند.
الف) چند ضلعی منتظم محدب ب) چند ضلعی منتظم پیچیده
- چند ضلعی های راست : چند ضلعی هایی که گوشه های راست داشته باشند. یعنی تمتم زاویه های داخلی آنها 90 یا 270 درجه باشد.
رياضيات همان شاه كليد گشودن رازهاي هستي است.
رياضيات به ذهن نظم مي بخشد و آدمي را به تفكر منطقي عادت مي دهد.
رياضيات هميشه و همه جا بلندگوي اين شعار است كه فعاليت آدمي پايان ناپذير است.
درك هر علمي مستلزم دانستن مقدماتي از علم رياضي مي باشد.
رياضيات عامل پيوستگي و ارتباط دهنده ي تمام ذرات كائنات است.
ریاضیات هم علم است و هم هنر. علم بدان معنا كه كشف مي كند و هنر بدان معنا كه زیباست.
رياضيات روح علوم است.
رياضيات دروازه و كليد علوم است.
هيچ شاخه اي از رياضيات نيست كه روزي در جهان واقعي به كار نرود.
معلمان ریاضی افتخاري مضاعف نصيبشان شده است كه در شاهراه بزرگ ترين رسالت بشري(معلمي) از بهترين وسيله ي حركتِ پيمودن مسير(يعني رياضيات ) استفاده مي كنند.
رياضيات زبان مشترك تمام آدم هاست.
رياضي راه و رسم زندگاني است و نمودارش خطوط مهرباني است.
رياضيات پايه ي علوم و زيربناي تفكر صحيح در جامعه است.
وضوح خطرناك ترين واژه در رياضيات است.
رياضيات خالص شده ي تمام علوم بشري است.
پويايي رياضيات در طرح سوالات نو و تعميم مسائل است.
مقدمه فاصله ی دو نقطه : فاصله ی دو نقطه طول پاره خطی است که دو نقطه را به هم وصل می کند.(تمرین 3 ص 60 کتاب) فاصله ی نقطه تا خط : کوتاه ترین فاصله ی یک نقطه تا یک خط ، طول خطی است که از آن نقطه بر خط عمود می شود.(تمرین 4 ص 60 کتاب) تعریف نیم ساز : نیم ساز خطی است که از راس زاویه می گذرد و زاویه را به دو قسمت مساوی تقسیم می کند. توجه :فاصله ی هر نقطه روی نیمساز یک زاویه از دو ضلع آن زاویه به یک فاصله است. انواع مثلث : 1-مثلث متساوی الاضلاع : مثلثی است که سه ضلع و سه زاویه ی مساوی دارد. و اندازه ی هر سه زاویه آن 60 درجه است. 2-مثلث متساوی الساقین : مثلثی که دو ضلع (دوساق)مساوی دارد.و دو زاویه ی مجاور آن دو ضلع برابرند. 3-مثلث قائم الزاویه : مثلثی که یک زاویه ی قائمه (90 درجه ) دارد. به ضلع روبرو به زاویه ی قائمهوتر می کویند. 4-مثلث قائم الزاویه ی متساوی الساقین : مثلثی که یک زاویه ی قائمه دارد و دو ضلع زاویه ی قائمه ی آن برابرند. 5-ملث مختلف الاضلاع : اندازه ی ضلع های آن باهم فرق دارند. ارتفاع خارجی :در مثلث مختلف الاضلاعی که یک زاویه ی باز دارد یک ارتفاع خارجی وجود دارد. توجه : مجموع زاویه های داخلی هر مثلث 180 درجه می باشد. ارتفاع مثلث : پاره خطی است که از یک راس ، عمود بر ضلع روبرو رسم می شود. توجه : در هر مثلث ، اندازه ی پاره خطی که وسط های دو ضلع یک مثلث را به هم وصل می کند نصف ضلع سوم است. (تمرین 2 ص 48 کتاب درسی) روی یک نیم خط یک نقطه بگذاریم 2 نیم خط به دست می آید اگر روی یک نیم خط 2 نقطه بگذاریم 4 نیم خط به دست می آید اگر روی یک نیم خط 3 نقطه بگذاریم 6 نیم خط به دست می آید اگر روی یک نیم خط 4 نقطه بگذاریم 8 نیم خط به دست می آید اگر روی یک نیم خط 5 نقطه بگذاریم 10 نیم خط به دست می آید دقت شود با روش بالا تعداد نیم خط ها به دست می آید نه تعداد پاره خط ها. ×××××××××××××××××××××××××××××××××××××××××××××××××××××××××× اندازه گیری زاویه : -وسیله ی اندازه گیری زاویه نقاله نام دارد. -واحد استاندارد اندازه گیری زاویه درجه نام دارد. -یک درجه برابر ( یک ، سیصدو شصتم ) -معنای زاویه : هر زاویه از دو نیم خط تشکیل شده است ، به نقطه ی مشترک این دونیم خط راس زاویه می گویند ، و به هر یک از این دو نیم خط ضلع زاویه می گویند. روش اندازه گیری زاویه با نقاله : (تمرین 5 ص 60 کتاب) نقطه ی شروع (صفر) نقاله را روی نقطه ی مشترک دو ضلع زاویه(راس زاویه) قرار می دهیم دقت کنیم که یک ضلع زاویه و خط شروع نقاله بر هم منطبق باشند. ضلع دیگر زاویه بر روی نقاله نشانگر اندازه ی زاویه می باشد. توجه : برای محاسبه ی مجموع زاویه های چند ضلعی ها ، چندتا از قطر های چند ضلعی را طوری رسم کنیم که همدیگر را قطع نکنند و شکل نیز به چند مثلث تبدیل شود حالا با ضرب تعداد مثلث ها در 180 درجه، مجموع زاویه های آن چند ضلعی به دست می آید. (تمرین 4 ص 59 کتاب درسی شش ضلعی) -ص 55 کتاب درسی تمرین 4 : اگر یک خط مورب دوخط موازی را قطع کند زاویه های مشخص شده روی شکل همیشه باهم برابر هستند. -ص 55 کتاب درسی تمرین 5 : همه ی زاویه هایی که راس آن ها روی دایره قرار داشته باشند و روبروی یک کمان از دایره باشند باهم مساوی هستند. انواع زاویه: زاویه ی رست یا قائمه که اندازه ی آن 90 درجه است.- زاویه ی تند که اندازه ی آن کمتر از 90 درجه است. – زاویه ی باز که اندازه ی آن بیشتر از 90 درجه است. زاویه ی نیم صفحه که اندازه ی آن 180 درجه است. -زاویه های متقابل به راس: اگر دو خط همدیگر را قطع کنند 4 زاویه به دست می آید که دو به دو برابر هستند این زاویه ها را متقابل به راس می گویند. ویژگی های دو زاویه ی متقابل به راس: (تمرین 6 ص 60 کتاب درسی) 1-دو زاویه ی متقابل به راس همیشه مساوی هستند. 2- راس آن ها روی هم قرار دارند.یعنی راس دو زاویه باید بر هم منطبق باشد. 3- ضلع هر یک در ادامه ی ضلع زاویه ی دیگر است. دو زاویه ی متمم و مکمل : (تمرین 7 ص 60 کتاب درسی) دو زاویه ی متمم :به دو زاویه ای که مجموع آن ها 90 درجه باشد دو زاویه ی متمم می گویند. مانند دوزاویه 20 درجه و 70 درجه . 90=20+70 دو زاویه ی مکمل : به هر دو زاویه ای که مجموع آن ها 180 درجه باشد دو زاویه ی مکمل می گویند. مانند دو زاویه ی 130 درجه و 50 درجه. 180=50+130 تبدیل واحد : (تمرین یک ص 60 کتاب و تو ضیح ص 44 کتاب درسی) برای تبدیل واحد های کوچک به بزرگ از ضرب در 10 ، 100 ، 1000 و... استفاده می کنیم و برای تبدیل واحدهای بزرگ به کوچک از تقسیم عدد بر 10 ، 100 ، 1000 و ..... استفاده می کنیم. سانتی متر210 = 1/2 متر
![]() یک دایره ی کامل است. به عبارت دیگر اگر یک دایره ی کامل را به 360 قسمت مساوی تقسیم کنیم هر قسمت آن یک درجه است.
یک دایره ی کامل است. به عبارت دیگر اگر یک دایره ی کامل را به 360 قسمت مساوی تقسیم کنیم هر قسمت آن یک درجه است.
دانلود نمونه سوالات آزمونهای نوبت دوم سری 1 پایهی ششم
آزمون املا نوبت دوم سری 1 + پاسخ نامه
آزمون نگارش و انشا نوبت دوم سری 1 +پاسخ نامه
آزمون هدیههای آسمان نوبت دوم سری 1 +پاسخ نامه
آزمون اجتماعی نوبت دوم سری1 +پاسخ نامه
آزمون علوم نوبت دوم سری 1 +پاسخ نامه
آزمون ریاضی نوبت دوم سری 1 +پاسخ نامه

منبع: شاهد بندر انزلی
تهیه شده توسط اداره سنجش آموزش و پرورش کشور
هدیههای آسمان ششم
بیش از ۲۵۰ نمونه سوال
حجم: ۹.۹ MB
علوم تجربی ششم
در حدود ۳۰۰ نمونه سوال
حجم: ۱۵.۳ MB
مطالعات اجتماعی
بیش از ۳۵۰ نمونه سوال
حجم:۱۲.۶ MB
فارسی ششم
بیش از ۳۳۰ نمونه سوال
حجم:۱۲.۶ MB
منبع : سایت آموزش ریاضی
با آنکه ممکن است چندان دل خوشی از درس ریاضیات نداشته باشید اما نقشی که این علم در زندگی روزمره هر انسان ایفا میکند را نمی توانید انکار کنید. اگر از جمله افرادی هستید که همیشه از درس ریاضیات متنفر بوده اند خیالتان راحت باشد؛ اینجا ما نمی خواهیم از معادلات حرف بزنیم، صرفا نگاهی به اعدادی خواهیم انداخت که در جهان شهرت خاصی برای خود رقم زده اند و مختصرا علت آن ها را بررسی می کنیم.

پاسخنامه آزمون ریاضی تا صفحه 30 آبان 92 ............ علی اسلامی
پاسخنامه آزمون ریاضی از فصل 1تا 2 ......................... علی اسلامی
پاسخنامه آزمون اجتماعی از درس 1 تا 8 ................... علیرضا بدرخجسته
پاسخنامه آزمون ریاضی فصل 3 ................................... علیرضا بدرخجسته
پاسخنامه آزمون کاروفناوری از درس 1تا 10 ............... ❀❀❀❀❀❀❀
پاسخنامه آزمون ریاضی از فصل 1تا 3 ......................... علی اسلامی
پاسخنامه آزمون بخوانیم و بنویسیم از درس 1تا 6..... علیرضا بدرخجسته
پاسخنامه آزمون ریاضی از فصل 1تا 4 ......................... رضا انصاریان
پاسخنامه آزمون علوم تجربی از درس 1تا 7................ علیرضا بدرخجسته
پاسخنامه آزمون هدیههای آسمان از درس 1تا 7....... محمدحسینبذربخش
پاسخنامه آزمون هدیههای آسمان از درس 1تا 10..... علیرضا بدرخجسته
پاسخنامه آزمون بخوانیم و بنویسیم از درس 1تا 10... علیرضا بدرخجسته
پاسخنامه آزمون اجتماعی از درس 1 تا 14 ................. علیرضا بدرخجسته
پاسخنامه آزمون ریاضی از صفحه 1 تا 91 ................... خرسندیان-انصاریان
پاسخنامه آزمون بخوانیم و بنویسیم 1تا 12.................. بدرخجسته-رحیمی
پاسخنامه آزمون علوم از درس 1 تا 8 .......................... اسدی-انصاری-حجتیپور
پاسخنامه آزمون ریاضی فصل 5 ................................... ❀❀❀❀❀❀❀❀
پاسخنامه آزمون ریاضی فصل 1 تا 5 (1 تا 100) ......... ❀❀❀❀❀❀❀❀
پاسخنامه آزمون هدیههای آسمان از درس 1تا 14...... رضا انصاریان
پاسخنامه آزمون علوم از درس 1 تا 10 ........................ رضا خرسندیان
پاسخنامه آزمون ریاضی فصل 1 تا 6 (1 تا 111) ......... ❀❀❀❀❀❀❀❀
پاسخنامه آزمون ریاضی فصل 1 تا 7 ............................ ❀❀❀❀❀❀❀❀
پاسخنامه آزمون بخوانیم و بنویسیم 1تا 14.................. بدرخجسته
پاسخنامه آزمون ریاضی فصل 1 تا 7 (متوسط) .......... ❀❀❀❀❀❀❀❀
پاسخنامه آزمون علوم از درس 1 تا 12 ........... بدرخجسته- انصاریان
پاسخنامه آزمون ریاضی فصل 1 تا 8 (متوسط) .......... ❀❀❀❀❀❀❀❀ 

1- حل مسئله یكی از روش های آموزش ریاضیات است.
2- در تدریس ریاضیات باید عوامل علاقه مندی كودكان به كلاس درس شناخته شود.
3- مبنای همه آموزش ها باید بر آزمایش استوار باشد. بخصوص آزمایش با مواد كمك آموزشی كه ساخته خود كودكان است.
4- گفتگو در مورد ریاضیات باید یكی از اهداف آموزش باشد.
5- این مفهوم كه بسیاری از اندیشه های ریاضیات با هم ارتباط دارند باید گسترش داده شود.
6- درك معنا و مفهوم در ریاضیات باید به عنوان زمینه ای در آموزش همواره مورد توجه قرارگیرد
7- كار گروهی در ریاضیات باید به یك روش معمول تبدیل شود.
8- نیازهای متفاوت كودكان باید مورد ملاحظه قرار گیرد.
9- برای كودكان باید فرصت هایی برابر در یادگیری ریاضیات فراهم شود.
10 - پیشرفت كودكان در زمینه ریاضیات باید از طریق آزمون های كتبی تشخیص داده شود.
امروزه مشاهده می كنیم كه در بیشتر مدارس معلمان به جای آنكه به كتاب های متعدد رجوع كنند یا حتی آنها را متناسب با نیازهای گروهی یا فردی تغییر دهند تنها از یك كتاب درسی برای همه دانش آموزان استفاده می كنند . كتاب های درسی زمینه یا چهارچوبی را فراهم می كنند كه از طریق آن می توانیم برنامه ریاضی محكم و استوار تدارك ببینیم. از طریق انجام آزمایش ، فعالیت های كلاسی و مواد آموزشی دست ساز می توان به آموزش ریاضیات یاری كرد.
دانش آموزان عزیز برای تقسیم اعداد اعشاری باید توجه داشته باشید که هیچ وقت مقسوم علیه نمی تواند یک عدد اعشاری باشد پس باید به یک عدد صحیح تبدیل شود ، آن هم به این صورت که مقسوم و مقسوم علیه را در عددی ضرب کنیم ( بدون اینکه تغییری در خارج قسمت ایجاد شود) پس با ضرب مقسوم و مقسوم علیه در ١۰، ١۰۰، ١۰۰۰و.....کاری می کنیم که اعشار مقسوم و مقسوم علیه از بین می رود و به یک عدد صحیح تبدیل می شود . حال با توجه به عمل تقسیم که قبلا" یاد گرفتید می توانید تقسیم را انجام داده ، اما تغییر دیگری که باید فراموش نشود این است که باقی مانده نیز غیر واقعی می باشد و باید باقی مانده را به همان عددی که در مقسوم و مقسوم علیه ضرب کردید یعنی: ١۰، ١۰۰، ١۰۰۰ تقسیم کنیم به این ترتیب در باقی مانده به همان تعداد رقمی که ممیز با ضرب به جلو آمده بود ، به عقب برمی گردد.
نویسنده : دانیال جهانگیری - دانش آموز پایه ششم
لطفا برای دانلوداینجایاروی تصویرزیرکلیک نمائید.
لطفا پس از دانلود و باز کردن پوشه
روی فایل omidvar.exe کلیک نمائید،
تا مشابه تصویر بالا باز شود.
حجم فایل 27,716 KB
فعالیتهای نرمافزاری ریاضی دوره ابتدایی
در این بخش نمونهای از فعالیتهای ریاضی دوره ابتدایی بهصورت نرمافزار طراحی شده که با کلیک بر روی هر عنوان میتوانید آن را اجرا نمایید. برای خروج از هر فعالیت از کلیدهای ترکیبی Alt + F4 استفاده کنید.
برای اجرا نیاز به نرم افزار فلش پلیر دارید دانلود کنید .
 دانلود:
دانلود:
کار با اشکال هندسی عملیات جمع
عملیات جمع با استفاده از محور
تفریق
شناخت اشکال هندسی
منبع: گروه ریاضی دفتر تالیف وکتب درسی
دانلود فلش پلیر :
توجه: اجرای هریک از این فعالیتها نیاز به نرمافزار Flash Player دارد لذا در صورتی که سیستم شما فاقد این نرمافزار است آن را از اینجا دانلود کنید:
 دانلود : Flash Player
دانلود : Flash Player
منبع : پیک آموزشی
انیمیشن های آموزشی کتاب ریاضی پایه ششم ابتدایی
انیمیشن های آموزشی فصل های سوم و پنجم کتاب ریاضی پایه ششم ابتدایی (اندازه گیری طول و زاویه – نسبت تناسب و درصد) به صورت فایل های فلش را از لینک های زیر دانلود نمایید.
ضمنا برای استفاده از این فایل ها باید نرم افزار فلش پلیر بر روی رایانه شما نصب شده باشد.
| انیمیشن های فصل سوم | ||
| انیمیشن های فصل پنجم (فایل های فلش ۱۰ – ۱) | ||
| انیمیشن های فصل پنجم (فایل های فلش ۲۰ – ۱۱) | ||
| انیمیشن های فصل پنجم (فایل های فلش ۳۰ – ۲۱) | ||
| انیمیشن های فصل پنجم (فایل های فلش ۴۰ – ۳۱) | ||
| انیمیشن های فصل پنجم (فایل های فلش ۵۰ – ۴۱) | ||
| انیمیشن های فصل پنجم (فایل های فلش ۵۸ – ۵۱) |
منبع »http://riazisara.ir/post/348
2- نمونه سوالات تیزهوشان ................
3- فرمول ها و راه حل های کاربردی ریاضی ششم
4- چندین نمونه سوال از آزمون ورودی مدارس استعدادهای درخشان و...
5- آزمون استعدادهای درخشان استان تهران
6- آزمون استعدادهای درخشان استان کرمان
7- آزمون جامع تیزهوشان ششم
8- نمونه سوالات تیزهوشان ششم پاسخ نامه
9-نمونه سوالات ریاضی تیزهوشان
10-سوالات گوناگون از آزمون تیزهوشان

بینهایت واقعا ذهن انسان را به چالش میکشاند. اولین ریاضیدانی که با آن دست و پنجه نرم کرد، ریاضیدان آلمانی گئورگ کانتور بود که پس از اندیشیدن بسیار طولانی مدت در مورد این پدیده ریاضی، سرانجام در سال 1918 در یک بیمارستان روانی از دنیا رفت. اما پیش از آنکه ذهن کانتور دچار فروپاشی شود، او توانسته بود کشفیات حیرت انگیزی را در خصوص بینهایت انجام دهد. اولین کشف این بود که تعداد زیادی بینهایت وجود دارد. در واقع، تعداد بی پایانی بینهایت وجود دارد که کانتور هر یک از آنها را یک عدد "ترانهایت" نام نهاده بود.
اولین بینهایت
اولین و به عبارتی "کوچکترین" بینهایت، بینهایتی است که اغلب ما آن را "بینهایت" تصور میکنیم. این بینهایتی است که با شمردن اعداد به سمت بالا و هرگز باز نایستادن به دست میآید: صفر، 1،2،3و... و این کار برای همیشه ادامه مییابد. کانتور این بینهایت را "الف-صفر" نامید که بخش اول نام آن از اولین حرف الفبای عبری گرفته شده است. تردید نیست که این بینهایت دارای خواصی بسیار عجیب است.
به عنوان مثال، افزودن عدد یک به الف- صفر، یا دو برابر کردن و یا به توان دو رساندن آن، هیچ تاثیری در مقدار آن ندارد و پاسخ همچنان الف- صفر خواهد بود. دلیل این امر آن است وقتی شما با چیزی بینهایت بزرگ سر و کار دارید، هیچ کاری مقدار آن تغییر دهد نمیتوانید انجام دهید.
اگر با این پاسخ متقاعد نشدهاید، روی یک ورق کاغذ دو دایره بکشید که قطر یکی دو برابر دیگری باشد. به بیان ریاضی، هر دایره از تعداد بی پایانی نقطه تشکیل شده است (زیرا نقطههای کوچک کوچکتر میشوند)، و محیط دایره برابر با عدد پی ضرب در اندازه قطر آن است. بنابراین محیط دایره بزرگتر دو برابر محیط دایره کوچکتری است که ترسیم کردهاند، در حالی که بنابر تعریف، هر دو دایره شامل تعداد بینهایت نقطهاند. به عبارت دیگر، دو برابر بینهایت هنوز هم بینهایت است، و حتی بینهایت برابر بینهایت باز همان بینهایت خواهد ماند.
هتل هیلبرت
نزدیک به آغاز قرن بیستم، یک ریاضیدان آلمانی دیگر به نام دیوید هیلبرت این واقعیت غیر عاید را به صورتی به تصویر کشید که تنها با بینهایت امکان این کار وجود دارد. ریاضیدانان هم اکنون مفهوم "هتل هیلبرت" را به کار میبرند، مهمانخانهای که تعداد اتاقهای آن برابر الف- صفر است و بنابراین هرگز اتاق خالی کم نمیآورد. حتی اگر تمام اتاقهای هتل هیلبرت را کرده باشند، صاحب هتل هنوز هم میتواند برای چند مسافر تازهای که از راه رسیدهاند اتاقث خالی پیدا کند، زیرا بینهایت به اضافه کمی بیشتر هنوز هم بینهایت است که برابر است با تعداد اتاقهای موجود در مهمانخانه. در حقیقت، حتی اگر با وجود پر بودن تمام اتاقهای مهمانخانه باز هم ناگهان سروکله بینهایت مسافر دیگر پیدا شود، هر یک از آنها میتوانند برای گذراندن شب خود یک اتاق خالی پیدا کنند، چون بینهایت به علاوه بینهایت باز هم بینهایت است.
بینهایت مطلق
کانتور بینهایتهای دیگری با خواصی بسیار عجیب تر را نیز یافته بود. "الف- یک" عددی آنچنان بزرگ است که هرگز نمیتوان به آن رسید، حتی ار شما تا ابد به شمردن ادامه دهید. پس از آن، تعداد بینهایتی از الفها و سار بینهایتها وجود دارند که سرانجام به بینهایتی میرسند که همه بینهایتهای دیگر را زیر چتر خود دارد. کانتور آن را "بینهایت مطلق" نامیده بود. این بینهایت چنان وسیع و بی کران است که اصلا نمیتوان آن را توصیف کرد. در واقع، تعریف آن بر این اندیشه استوار است که هر تلاشی برای توصیف آن، همواره به توصیف چیزی کوچکتر میانجامد.
آخرین یافتهها در مورد بینهایت
حدود یک قرن طول کشیده است تا ریاضیدانان روشهایی را برای سر و کله زدن با بینهایت بیابند که در میانه راه آنها را به دیوانگی نکشاند. در اوایل دهه 1970، ریاضیدانان انگلیسی جان کانوی که هم اکنون در دانشگاه پرینستون حضور دارد، گونه جدیدی از اعداد را موسوم به "اعداد فراواقعی" کشف کرد که علاوه بر تمامی اعداد معمول، اعداد موسوم به ترانهایت و بسیاری از اعداد یر عادی دیگر را نیز شامل میشود. در نتیجه این کشف، ریاضیدانان هم اکنون میتوانند به عنوان مثال، ریشه دوم بینهایت را محاسبه کنند و یا لگاریتم آن را به دست آورند. بدون اینکه به پاسخهایی کاملا بیمعنا دست یابند.
حتی با این وجود نیز اغلب ریاضیدانان مایلند کاری به کار بینهایت نداشته باشند. بینهایت یک مشکل آفرین واقعی است، که میتواند پرسشهای معقول را به پاسخهایی کاملا بی ربط و غیر عادی 0 همچون 1=0 تبدیل کند. اما دانشمندانی که در ماهیت بنیادی عالم کند و کاو میکنند، در محاسبات خود مرتب به بینهایت برخورد میکنند. معمولا در چنین مواقعی آنها باید تسلیم بینهایت شوند، و یا اینکه برای بیرون راندن بینهایت مزاحم از نتیجه محاسبات خود عذری بتراشند که در نهایت کار جالبی نیست. اما ریاضیدانان برجستهای همچون کانوی و مارتین کروسکال از دانشگاه را تجرز در نیوجرسی، امیدوارند که روزی اعداد فراواقعی برجستنهای همچون کانوی و مارتین کروسکال از دانشگاه را تجرز در نیوجرسی، امیدوارند که روزی اعداد فراواقعی دانشمندان را در برخورد با این مسائل مربوط به بینهایت یاری دهند، و به آنها امکان دهند تا پاسخهایی واقعی را برای معماهای عالم بیابند، البته به شرط آنکه کلانجار رفتن با این مسائل آنها را دیوانه نکرده باشد.
منبع:www.daneshju.ir
شاید تا به حال به این فکر کرده باشید که بعد از میلیارد چیست؟؟
ترتیب بدین صورت است که بعد از هزار و میلیون میلیارد داریم که بیلیارد هم خوانده می شود و بعد از آن بیلیون و تریلیون و ... را داریم. به طور کلی اعداد را می توان در جدول زیر مشاهده کرد.
البته این جدول را می توان تا 100 مورد نوشت که آخرین آن 10600 است که قابل تصور هم نیست.
| Worldجهان | USآمریکا | n زیلیون | nth zillion | n |
| 106 | 106 | میلیون | Million | 1 |
| 109 | میلیارد | Milliard | 2 | |
| 1012 | 109 | بیلیون | Billion | 3 |
| 1018 | 1012 | تریلیون | Trillion | 4 |
| 1024 | 1015 | کوادریلیون | Quadrillion | 5 |
| 1030 | 1018 | کوینتیلیون | Quintillion | 6 |
| 11036 | 1021 | سیکستیلون | Sextillion | 7 |
| 1042 | 1024 | سپتیلیون | Septillion | 8 |
| 1048 | 1027 | اکتیلیون | Octillion | 9 |
| 1054 | 1030 | نونیلیون | Nonillion | 10 |
| 1060 | 1033 | دسیلیون | Decillion | 11 |
| 1066 | 1036 | آندسیلیون | Undecillion | 12 |
| 1072 | 1039 | دودسیلیون | Dodecillion | 13 |
| 1078 | 1042 | تریدسیلیون | Tredecillion | 14 |
| 1084 | 1045 | کواتردسیلیون | Quattuordecillion | 15 |
| 1090 | 1048 | کویندسیلیون | Quindecillion | 16 |
| 1096 | 1051 | سیکسدسیلیون | Sexdecillion | 17 |
| 10102 | 1054 | سپتندسیلیون | Septendecillion | 18 |
| 10108 | 1057 | اکتودسیلیوم | Octodecillion | 19 |
|
10114 |
1060 | نومدسیلیون | Novemdecillion | 20 |
1- به موضوع درس خود ،علاقه مند باشید .
۲- بر ماده درسی خود، مسلّط باشید .
۳- بدانید، از چه راهی می توانید آنچه را در نظر دارید، یاد بدهید؟ بهترین روش یاددادن را خودتان پیدا کنید .
۴- به چهره شاگردان خود نگاه کنید، تا متوجه انتظارهای آنها بشوید . دشواری های آنها
را کشف کنید؛ توانایی این را داشته باشید که بتوانید خودتان را به جای آنان بگذارید .
۵-به آگاهی های خشک قناعت نکنید. بکوشیدمهارت راکه لازمه عقل و اندیشه است و
عادت به کار منظم را، در دانش آموزان تقویت کنید و تکامل بخشید.
۶- بکوشید تا حدس زدن و پیش بینی کردن را به آنان بیاموزید.
۷- سعی کنید، اثبات کردن را به دانش آموزان یاد بدهید.
۸- در مسأله ای که طرح شده است ، چیزی را جستجو کنید که، برای حل مسأله های
دیگر مفید است . از موقعیتی که مسأله مشخص مفروض دارد ،روش کلی را کشف
کنید .
۹- راز خود را ، بلافاصله فاش نکنید . اجازه بدهید دانش آموزان تا آنجا که می توانند
تلاش خود را برای حل یا حدس راه حل ، به کار برند ؛ به دانش آموزان امکان بدهید
،هر چه بیشتر خودشان کشف کنند .
۱۰- با اشاره های خود ، دانش آموزان را راهنمایی کنید، ولی عقیده خود را ، به زور
به آنها تحمیل نکنید .
از گذشته تا حال
آيا مي دانستيد مغز شما به دو قسمت تقسيم شده است كه اين دو قسمت از هم جدا هستند. در دو هزار سال پيش بشر چيزي راجع به مغز نمي دانست . قبل از يونانيها فكر به بدن متصل نبود و بعنوان بخار يا گاز يا روح جدا از بدن تلقي مي شد. يونانيها بيش از این نمي دانستند و حتي ارسطو متفكر معروف فلسفه و باني علوم قديم چنين گفته است كه مركز احساسات و حافظه در قلب است. از زمان يونانيها تا رسانس هيچ پيشرفتي دراين عقيده بوجود نيامد....
بقيه ي مطالب را در ادامه ي مطالب مشاهده بفرماييد

آیا تا به حال فکر کرده اید چرا زنبور عسل، خانه اش را بصورت شش ضلعی منتظم می سازد؟!
بقیه در ادامه مطلب
شمارش يوناني:
10 9 8 7 6 5 4 3 2 1
دكا ننا اكتا هپتا هگزا پنتا تترا تري دي منو
در شکل زیر چند مثلث میبینید؟
راهنمایی: گول ظاهر ساده سوال را نخورید.

اما پاسخ صحیح:
همانطور که تعداد زیادی از اعضا پاسخ صحیح داده بودند، تعداد مثلثها ۲۷ عدد است. ۱۶ مثلث تکی+ ۷ مثلث چهارتایی+۳ مثلث نه تایی و ۱ مثلث بزرگ = ۲۷ عدد
طریقه حساب کردن

۶۵=۶۴ !!!!!!!
65 = 64 شايد باور کردنش سخت باشه ولي طبق استدلالي که در اين تصوير متحرک بيان شده
تعجب نکنید ۶۴ با ۶۵ برابر است
شصت و چهار مساويست با شصت و پنج !!!


روی میزی پنج جسم قرار دهید , طوریکه تعداد حروف تشکیل دهنده اسم
اجسام از 9 بیشتر نباشد و اجسام از نظر تعداد حروف یکسان هم نباشند.
مانند کاغذ که چهار حرفی است و خودنویس که هفت حرفی است. سپس
از حاضرین تقاضا کنید که دور از چشم شما پنج جسم درکاغذی لیست کنند
بطوریکه تعداد حروفشان برابر نباشد. سپس بصورتی که شما دستور می دهید
عمل نمایند.
نحوه عمل
- اسم یکی از پنج جسم را به دلخواه در ذهن خود انتخاب نمایند.
- تعداد حروف آنرا در عدد 5 ضرب کنند.
- به این حاصلضرب عدد 3 را اضافه کنند.
- حاصل جمع به دست آمده را در عدد 2 ضرب کنند.
- به حاصل ضرب بدست آمده رقم دلخواهی (از 1 تا 9) اضافه نمایند.
- نتیجه را به شما بگویند، تا شما بطور غیبی بگویید که آنها کدام جسم را انتخاب کردهاند و چه رقم دلخواهی رویش اضافه نموده اند.
- عدد نهاییگزارش شده به شما که بدون شک دو رقمی میباشد .
- از این عدد بطور ذهنی عدد 6 را کم کنید.
پیش گویی غیبی
رقم دهگان این عدد تعداد حروف جسم مفروض و در نتیجه خود جسم
را مشخص میکند .
رقم یکان این عدد , عدد دلخواه اضافه شده به این محاسبات را معین میکند .
در این کار علاوه از ریاضیات پیش گویی غیبی و شعبده بازی نیز یاد گرفتهاید
.: Weblog Themes By Pichak :.





















 و نوشتنی در کار نباشددرصد موفقیت
و نوشتنی در کار نباشددرصد موفقیت 
 آمار
وب سایت:
آمار
وب سایت:

